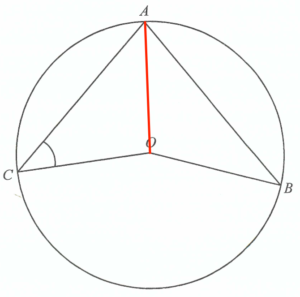
Join $OA$.
$\begin{array}{rcll}
\angle CAB & = & \dfrac{1}{2} \angle BOC & \text{($\angle$ at centre twice $\angle$ at $\unicode{x2299}^{ce}$)} \\
\angle CAB & = & \dfrac{1}{2} \times 164^\circ \\
\angle CAB & = & 82^\circ
\end{array}$
In $\Delta OAB$,
$\begin{array}{rcll}
\because OA & = & OB & \text{(radii)} \\
\therefore \angle OAB & = & \angle OBA & \text{(base $\angle$s, isos. $\Delta$)} \\
\angle OAB & = & 36^\circ
\end{array}$
In $\Delta OCA$,
$\begin{array}{rcll}
\because OA & = & OC & \text{(radii)} \\
\therefore \angle OCA & = & \angle OAC & \text{(base $\angle$s, isos. $\Delta$)} \\
\angle OCA & = & \angle CAB -\angle OAB \\
\angle OCA & = & 82^\circ -36^\circ \\
\angle OCA & = & 46^\circ
\end{array}$

