Ans: D
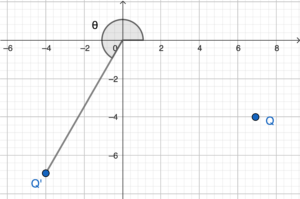

Note that the rectangular coordinates of the image $Q’$ are $(-4, -4\sqrt{3})$.
$\begin{array}{rcl}
\tan \theta & = & \dfrac{-4\sqrt{3}}{-4} \\
\tan \theta & = & \sqrt{3} \\
\theta & = & 60^\circ \text{ or } 240^\circ
\end{array}$
Since $Q’$ lies in quadrant III, then $\theta = 240^\circ$.
$\begin{array}{rcl}
OQ’ & = & \sqrt{(-4)^2 +(-4\sqrt{3})^2} \\
OQ’ & = & 8
\end{array}$
Therefore, the polar coordinates of $Q’$ is $(8, 240^\circ)$.

