Ans: D
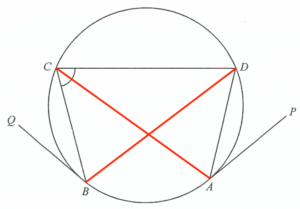

Join $AC$ and $BD$.
$\begin{array}{rcll}
\angle BDC & = & \angle CBQ & \text{($\angle$ in alt. segment)} \\
\angle BDC & = & 39^\circ \\
\angle ADB & = & \angle ADC -\angle BDC \\
\angle ADB & = & 79^\circ -39^\circ\\
\angle ADB & = & 40^\circ
\end{array}$
Also,
$\begin{array}{rcll}
\angle ACB & = & \angle ADB & \text{($\angle$s in the same segment)} \\
\angle ACB & = & 40^\circ
\end{array}$
Furthermore,
$\begin{array}{rcll}
\angle ACD & = & \angle DAP & \text{($angle$ in alt. segment)} \\
\angle ACD & = & 42^\circ
\end{array}$
Therefore, we have
$\begin{array}{rcl}
\angle BCD & = & \angle ACD +\angle ACB \\
\angle BCD & = & 42^\circ +40^\circ \\
\angle BCD & = & 82^\circ
\end{array}$

