2023-I-12

$\begin{array}{rcl}
f(10) & = & 62 \\
k_1+k_2(10)^2 & = & 62 \\
k_1 +100k_2 & = & 62 \ldots \unicode{x2460}
\end{array}$

Also,

$\begin{array}{rcl}
f(15) & = & 122 \\
k_1 +k_2(15)^2 & = & 122 \\
k_1 +225k_2 & = & 122 \ldots \unicode{x2461}
\end{array}$

$\unicode{x2461} -\unicode{x2460}$, we have

$\begin{array}{rcl}
125k_2 & = & 60 \\
k_2 & = & \dfrac{12}{25}
\end{array}$

Sub. $k_2=\dfrac{12}{25}$ into $\unicode{x2460}$, we have

$\begin{array}{rcl}
k_1 +100\left(\dfrac{12}{25} \right) & = & 62 \\
k_1 & = & 14
\end{array}$

Therefore, $f(x) =14+\dfrac{12}{25}x^2$.

Hence, we have

$\begin{array}{rcl}
f(5) & = & 14 +\dfrac{12}{25} \times (5)^2 \\
f(5) & = & 26
\end{array}$

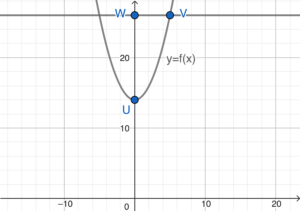
Note that $U$ is the $y$-intercept of the graph of $y=f(x)$, then the coordinates of $U$ are $(0,14)$.

By the result of (a), the coordinates of $V$ are $(5,26)$.

Since $\angle UWV=90^\circ$, then $UV$ is a diameter of $C$.

The radius of $C$

$\begin{array}{cl}
= & \dfrac{1}{2} UV \\
= & \dfrac{1}{2} \sqrt{(5-0)^2+(26-14)^2} \\
= & \dfrac{13}{2}
\end{array}$

Hence, the circumference of $C$

$\begin{array}{cl}
= & 2\pi \times \dfrac{13}{2} \\
= & 13\pi
\end{array}$