2023-I-14

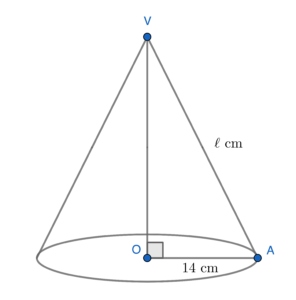
Let $\ell \text{ cm}$ be the slant height of the cone. Then we have

$\begin{array}{rcl}
\pi (14)(\ell) & = & 700\pi \\
\ell & = & 50
\end{array}$

Therefore, the slant height of the cone is $50\text{ cm}$.

The height of the cone

$\begin{array}{cl}
= & \sqrt{50^2 -14^2} \\
= & 48\text{ cm}
\end{array}$

1. Sketch the graph according to the question.
   

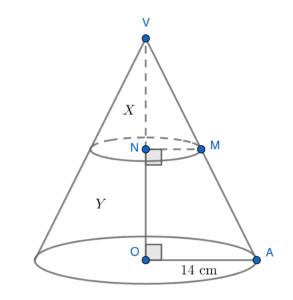
   The volume of the original cone

   $\begin{array}{cl}
   = & \dfrac{1}{3} \pi(14)^2(48) \\
   = & 3136\pi \text{ cm}^3
   \end{array}$

   The surface area of $X$

   $\begin{array}{cl}
   = & 700\pi \times \dfrac{1}{1+15} \\
   = & \dfrac{175}{4}\pi\text{ cm}^2
   \end{array}$

   Since $X$ and the original cone are similar to each other, we have

   $\begin{array}{rcl}
   \left(\dfrac{\text{volume of the original cone}}{\text{volume of $X$}}\right)^2 & = & \left(\dfrac{\text{curved surface area of the original cone}}{\text{curved surface area of $X$}}\right)^3 \\
   \left( \dfrac{3136\pi}{\text{volume of $X$}}\right)^2 & = & \left( \dfrac{700\pi}{\frac{175}{4}\pi}\right)^3 \\
   \text{volume of $X$} & = & 49\pi \text{ cm}^3
   \end{array}$

   Hence, the volume of $Y$

   $\begin{array}{cl}
   = & 3136\pi -49\pi \\
   = & 3087\pi\text{ cm}^3
   \end{array}$

2. Let $r\text{ cm}$ be the radii of the spheres.

   $\begin{array}{rcl}
   2 \times \dfrac{4}{3} \pi r^3 & = & 3087\pi \\
   r^3 & = & \dfrac{9261}{8} \\
   r & = & \dfrac{21}{2}
   \end{array}$

   Hence, the diameter of the spheres

   $\begin{array}{cl}
   = & 2 \times \dfrac{21}{2} \\
   = & 21\text{ cm}
   \end{array}$