2023-I-17

$\begin{array}{rcl}
\dfrac{WX}{\sin \angle WYX} & = & \dfrac{XY}{\sin \angle XWY} \\
\dfrac{6}{\sin 70^\circ} & = & \dfrac{5}{\sin \angle XWY} \\
\sin \angle XWY & = & \dfrac{5\sin 70^\circ}{6} \\
\angle XWY & = & 51.543\ 189\ 37^\circ
\end{array}$

It is given that the angle between $WZ$ and $\Delta WXY$ is $30^\circ$. Then $\angle ZWZ’ =30^\circ$. In $\Delta WZZ’$, we have

$\begin{array}{rcl}
\tan \angle ZWZ’ & = & \dfrac{ZZ’}{WZ’} \\
ZZ’ & = & WZ’ \tan 30^\circ \ldots \unicode{x2460}
\end{array}$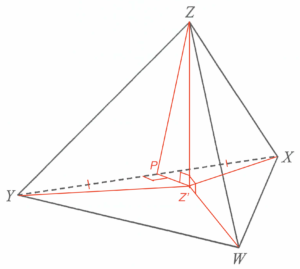

Let $P$ be the mid-point of $XY$.

Since $WZ=XZ=YZ$, then $WZ’=XZ’=YZ’$. Therefore, $Z’$ is the circumcentre of $\Delta WXY$.

Hence, $PZ’$ is the perpendicular bisector of $XY$.

Therefore, the angle between $\Delta WXY$ and $\Delta XYZ$ is $\angle ZPZ’$.

Since $Z’$ is the circumcentre of $\Delta WXY$, then $\angle XZ’Y = 2 \angle XWY$ ($\angle$ at centre twice $\angle$ at $\unicode{x2299}^{ce}$).

Note that $\Delta PXZ’ \cong \Delta PYZ’$, then $\angle PZ’X = \angle PZ’Y$ (corr. $\angle$s, $\cong\Delta$s).

Hence, $\angle PZ’Y = \angle XWY$.

In $\Delta PYZ’$,

$\begin{array}{rcl}
\cos \angle PZ’Y & = & \dfrac{PZ’}{YZ’} \\
PZ’ & = & YZ’ \cos \angle PZ’Y \\
PZ’ & = & WZ’ \cos \angle XWY \ldots \unicode{x2461}
\end{array}$

In $\Delta PZZ’$,

$\begin{array}{rcll}
\tan \angle ZPZ’ & = & \dfrac{ZZ’}{PZ’} \\
\tan \angle ZPZ’ & = & \dfrac{WZ’ \tan 30^\circ}{ WZ’ \cos \angle XWY} & \text{, by $\unicode{x2460}$ and $\unicode{x2461}$} \\
\tan \angle ZPZ’ & = & \dfrac{\tan 30^\circ}{\cos 51.543\ 189\ 37^\circ} \\
\angle ZPZ’ & = & 42.871\ 428\ 55^\circ \\
\angle ZPZ’ & < &45^\circ \end{array}$

$\therefore$, the angle between $\Delta WXY$ and $XYZ$ does not exceed $45^\circ$.