2023-I-19

$\begin{array}{rcl}
32 & = & \dfrac{a+50}{2} \\
64 & = & a +50 \\
a & = & 14
\end{array}$

Also,

$\begin{array}{rcl}
t & = & \dfrac{b+0}{2} \\
b & = & 2t
\end{array}$

Therefore, $R=(14,2t)$.

Since $OP$ is a horizontal line, then $RH$ is a vertical line. Hence, the $x$-coordinate of $H$

$\begin{array}{cl}
= & x\text{-coordinate of $R$} \\
= & 14
\end{array}$

Let $H=(14,d)$. Since $OH \perp PR$, then we have

$\begin{array}{rcl}
m_{OH} \times m_{PR} & = & -1 \\
\dfrac{d-0}{14-0}\times \dfrac{2t-0}{14-50} & = & -1 \\
dt & = & 252 \\
d & = & \dfrac{252}{t}
\end{array}$

Therefore, the coordinates of $H$ are $\left(15, \dfrac{252}{t}\right)$.

Since $OP$ is a horizontal line, then the perpendicular bisector of $OP$ is a vertical line. Hence, the $x$-coordinate of $G$

$\begin{array}{cl}
= & \dfrac{0+50}{2} \\
= & 25
\end{array}$

Let $G=(25,c)$. Since $Q$ is the mid-point of $PR$, then $GQ$ is the perpendicular bisector of $PR$. Hence, we have

$\begin{array}{rcl}
m_{GQ} \times m_{PR} & = & -1 \\
\dfrac{c-t}{25-32} \times \dfrac{2t-0}{14-50} & = & -1 \\
t(c-t) & = & -126 \\
c & = & t-\dfrac{126}{t} \\
c & = & \dfrac{t^2-126}{t}
\end{array}$

Therefore, the coordinates of $G$ are $\left(25, \dfrac{t^2-126}{t} \right)$.

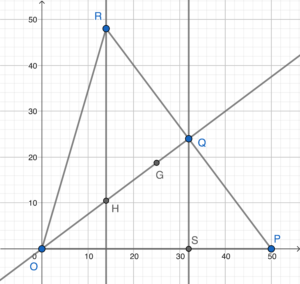
1. Since $\angle PQS = \angle POQ$, then we have

   $\begin{array}{rcl}
   \tan \angle PQS & = & \tan \angle POQ \\
   \dfrac{PS}{QS} & = & \dfrac{QS}{SO} \\
   \dfrac{50-32}{t-0} & = & \dfrac{t-0}{32-0} \\
   t^2 & = & 576
   \end{array}$

   $\therefore t=24$ or $t=-24$ (rejected).

2. Note that the coordinates of $G$ and $Q$ are $\left(25, \dfrac{75}{4}\right)$ and $(32,24)$ respectively.

   The slope of $OG$

   $\begin{array}{cl}
   = & \dfrac{\frac{75}{4}-0}{25-0} \\
   = & \dfrac{3}{4}
   \end{array}$

   The slope of $OQ$

   $\begin{array}{cl}
   = & \dfrac{24-0}{32-0} \\
   = & \dfrac{3}{4}
   \end{array}$

   Since $m_{OG} =m_{OQ}$ and $O$ is the common point, then $O$, $G$ and $Q$ are collinear.

3. Add the angle bisector of $\angle OPR$ to the graph. Let $J$ be the foot of perpendicular of $I$ on $OP$.
   

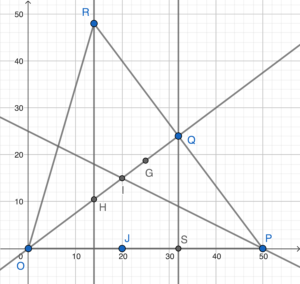
   Since $OQ\perp PQ$ and $IJ \perp OP$, then $QP$ and $JP$ are tangents to the inscribed circle of $\Delta OPR$ at $Q$ and $J$ respectively.

   $\begin{array}{rcl}
   QP & = & \sqrt{(32-50)^2+(24-0)^2} \\
   QP & = & 30
   \end{array}$

   Therefore, the coordinates of $J$ are $(50-30, 0)$, i.e. $(20,0)$.

   Since $IJ$ is a vertical line, then the $x$-coordinates of $I$ and $J$ are equal. Let $I=(20,e)$.

   Note that $IJ$ and $IQ$ are radii of the inscribed circle of $\Delta OPR$.

   $\begin{array}{rcl}
   IJ & = & IQ \\
   e & = & \sqrt{(32-20)^2+(24-e)^2} \\
   e^2 & = & 144 +576-48e+e^2 \\
   48e & = & 720 \\
   e & = & 15
   \end{array}$

   Therefore, the coordinates of $I$ are $(20,15)$.

   By the result of (a) and (b)(i), the coordinates of $H$ are $\left(14,\dfrac{21}{2}\right)$.

   Since $OQ$ is the perpendicular bisector of $PR$, then we have $PQ=RQ$ and $OQ\perp PR$.

   $\begin{array}{cl}
   & \text{area of $\Delta GHR$} : \text{area of $\Delta IPQ$} \\
   = & \dfrac{1}{2}(GH)(RQ) : \dfrac{1}{2} (IQ)(PQ) \\
   = & GH : IQ \\
   = & \sqrt{(25-14)^2+\left(\dfrac{75}{4}-\dfrac{21}{2}\right)^2} : \sqrt{(32-20)^2+(24-15)^2} \\
   = & \dfrac{55}{4} : 15 \\
   = & 11 : 12
   \end{array}$