Join $R$ and $X$. Let $PX:XQ =r:1$, where $r>0$.
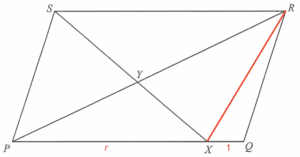
Since $\Delta PQR$ and $\Delta RQX$ have the same height with respect to the base $PX$ and $XQ$ respectively, then we have
$\begin{array}{rcl}
\dfrac{\text{area of $\Delta PQR$}}{\text{area of $\Delta QRX$}} & = & \dfrac{PQ}{XQ} \\
\dfrac{32+58}{\text{area of $\Delta QRX$}} & = & \dfrac{1+r}{1} \\
\text{area of $\Delta QRX$} & = & \dfrac{90}{1+r}
\end{array}$
Since $\Delta PXY \sim \Delta RSY$, then we have
$\begin{array}{rcl}
\dfrac{PY}{RY} & = & \dfrac{PX}{RS} \\
\dfrac{PY}{RY} & = & \dfrac{r}{1+r}
\end{array}$
Since $\Delta PXY$ and $\Delta RXY$ have the same height with respect to the base $PY$ and $RY$ respectively, then we have
$\begin{array}{rcl}
\dfrac{\text{area of $\Delta PXY$}}{\text{area of $\Delta RXY$}} & = & \dfrac{PY}{RY} \\
\dfrac{32}{\text{area of $\Delta RXY$}} & = & \dfrac{r}{1+r} \\
\text{area of $\Delta RXY$} & = & \dfrac{32(1+r)}{r}
\end{array}$
Hence, we have
$\begin{array}{rcl}
\text{area of $\Delta QRX$}+\text{area of $\Delta RXY$} & = & \text{area of $QRYX$} \\
\dfrac{90}{1+r}+\dfrac{32(1+r)}{r}& = & 58 \\
90r+32(1+r)^2 & = & 58r(1+r) \\
90r +32+64r+32r^2 -58r-58r^2 & = & 0 \\
-26r^2+96r+32 & = & 0 \\
13r^2-48r-16 & = & 0 \\
(r-4)(13r+4) & = & 0
\end{array}$
$\therefore r=4$ or $r=\dfrac{-4}{13}$ (rejected).
Since $\Delta PXY \sim \Delta RSY$, then we have
$\begin{array}{rcl}
\dfrac{\text{area of $\Delta PXY$}}{\text{area of $\Delta RSY$}} & = & \left(\dfrac{PX}{RS}\right)^2 \\
\dfrac{32}{\text{area of $\Delta RSY$}} & = & \left(\dfrac{4}{1+4}\right)^2 \\
\text{area of $\Delta RSY$} & = & 50 \text{ cm}^2
\end{array}$

