Ans: A
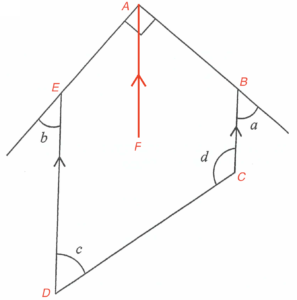
Denote the vertex by $A$, $B$, $C$, $D$ and $E$ as shown in the figure.

I must be true. Add a point $F$ such that $ED\text{//}AF\text{//}BC$.
Hence, we have $\angle EAF=b$ and $\angle BAF =a$. Therefore, $a+b=90^\circ$.
II must be true. Since $BC\text{//}ED$, $c+d=180^\circ$.
III may not be true. If $c=30^\circ$, then by II, $d=150^\circ$. Hence, we have
$\begin{array}{cl}
& a+b+c \\
= & 90^\circ+30^\circ\\
= & 120^\circ \\
\neq & d
\end{array}$

