Ans: C
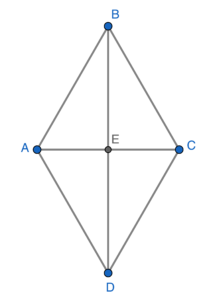

I may not be true. By the definition of rhombus, $AB=BC=CD=DA$. Refer to the figure, it is obvious that $AE\neq BE$.
II must be true. Since rhombus is a parallelogram, then the diagonals bisect each other. Therefore, $AC=2AE$ and $BD=2BE$. Hence, we have
$\begin{array}{rcl}
\dfrac{AE}{AC} & = & \dfrac{BE}{BD} & = & \dfrac{1}{2}
\end{array}$
III must be true. $\angle AEB=90^\circ$ is a property of rhombus. Then we have
$\begin{array}{rcl}
AE^2 +BE^2 & = & AB^2 \\
AE^2+BE^2 & = & CD^2
\end{array}$

