A is not true. Consider $\Delta RTV$. It is given that $RT=RV$, then $\angle RTV = \angle RVT$.
If $RV\text{//}ST$, then $\angle RVT = \angle PTS =90^\circ$. It is impossible that $\angle RTV=\angle RVT=90^\circ$. Hence, $RV$ is not parallel to $ST$.
B may not be true. Sketch a graph according to the question.
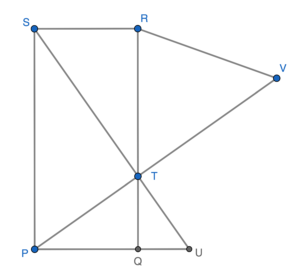
From the sketch, it is obviously that $\angle PTQ \neq \angle RTS$.
C must be true. In $\Delta PST$ and $\Delta UTQ$,
$\begin{array}{rcll}
\angle PQT & = & 90^\circ &\text{(properties of rectangle)} \\
\angle UQT & = & 180^\circ -\angle PQT & \text{(adj. $\angle$s on a st line)} \\
\angle UQT & = & 180^\circ -90^\circ \\
\angle UQT & = & 90^\circ \\
\angle UQT & = & \angle PTS &\text{(given)}
\end{array}$
Also,
$\begin{array}{rcll}
PS & \text{//} & QR & \text{(properties of rectangle)} \\
\angle PST & = & \angle UTQ & \text{(corr. $\angle$s, $PS$//$QR$)}
\end{array}$
$\therefore \Delta PST \sim \Delta UTQ$ (A.A.).
D may not be true. According to the sketch in option B, $\Delta PQT \not \cong \Delta TRS$.

