Ans: C
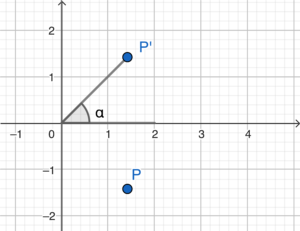
Denote the image of $P$ by $P’$.

Note that the rectangular coordinates of $P’$ are $(\sqrt{2},\sqrt{2})$.
$\begin{array}{cl}
& OP’ \\
= & \sqrt{(\sqrt{2})^2 +(\sqrt{2})^2} \\
= & 2
\end{array}$
Also,
$\begin{array}{rcl}
\tan \alpha & = & \dfrac{\sqrt{2}}{\sqrt{2}} \\
\tan \alpha & = & 1 \\
\alpha & = & 45^\circ
\end{array}$
Therefore, the polar coordinates of $P’$ are $(2, 45^\circ)$.

