Join $P$ and $R$.
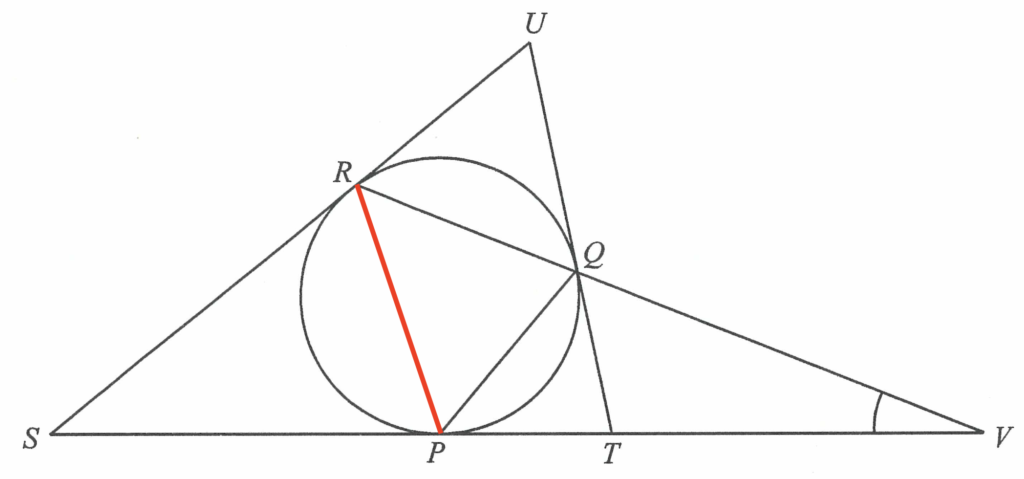
Since $SU$ and $ST$ are tangent to the circle at $R$ and $P$ respectively, then we have
$\begin{array}{rcll}
SR & = & SP & \text{(tangent properties)} \\
\therefore \angle SRP & = & \angle SPR & \text{(base $\angle$s, isos. $\Delta$)} \\
\angle SRP & = & \dfrac{1}{2} (180^\circ -\angle PSR) & \text{($\angle$ sum of $\Delta$)} \\
\angle SRP & = & \dfrac{1}{2}(180^\circ-34^\circ) \\
\angle SRP & = & 73^\circ
\end{array}$
Also,
$\begin{array}{rcll}
\angle PRQ & = & \angle QPT & \text{($\angle$ in alt. segment)} \\
\angle PRQ & = & 46^\circ
\end{array}$
In $\Delta RSV$, we have
$\begin{array}{rcll}
\angle PVQ & = & 180^\circ -\angle RSV-\angle SRP-\angle PRV & \text{($\angle$ sum of $\Delta$)} \\
\angle PRV & = & 180^\circ-34^\circ-73^\circ-46^\circ \\
\angle PRV & = & 27^\circ
\end{array}$

