Add a point $X$ on $VB$ such that $AX\perp VB$ and $CX\perp VB$. Then the angle between $\Delta VAB$ and $\Delta VBC$ is $\angle AXC$.
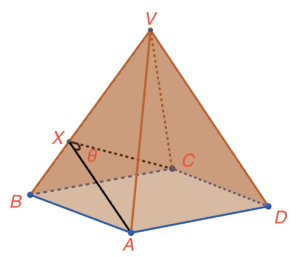
Since $AB:AV=5:4$, then let $AB=5k$ and $AV=4k$, for some $k\neq 0$. Since $VABCD$ is a right pyramid with square base, then $AB=BC=CD=DA=5k$ and $VA=VB=VC=VD=4k$.
In $\Delta VAB$, we have
$\begin{array}{rcl}
\cos \angle VBA & = & \dfrac{AB^2+VB^2-VA^2}{2(AB)(VB)} \\
\cos \angle VBA & = & \dfrac{(5k)^2+(4k)^2-(4k)^2}{2(5k)(4k)} \\
\cos \angle VBA & = & \dfrac{5}{8}
\end{array}$
In $\Delta ABX$, we have
$\begin{array}{rcl}
\sin \angle ABX & = & \dfrac{AX}{AB} \\
AX & = & AB \sin \angle ABX \\
AX & = & 5k \sqrt{1-\cos^2 \angle ABX} \\
AX & = & 5k \sqrt{1-\left(\dfrac{5}{8}\right)^2} \\
AX & = & 5k \sqrt{1-\dfrac{25}{64}} \\
AX & = & \dfrac{5\sqrt{39}}{8} k
\end{array}$
Similarly, $CX=\dfrac{5\sqrt{39}}{8} k$.
In $\Delta ABC$, we have
$\begin{array}{rcl}
AC^2 & = & AB^2 +BC^2 \\
AC^2 & = & (5k)^2+(5k)^2 \\
AC & = & \sqrt{50} k
\end{array}$
In $\Delta ACX$, we have
$\begin{array}{rcl}
\cos \angle AXC & = & \dfrac{AX^2+CX^2-AC^2}{2(AX)(CX)} \\
\cos \theta & = & \dfrac{(\frac{5\sqrt{39}}{8}k)^2+(\frac{5\sqrt{39}}{8}k)^2-(\sqrt{50}k)^2}{2(\frac{5\sqrt{39}}{8}k)(\frac{5\sqrt{39}}{8}k)} \\
\cos \theta & = & \dfrac{-25}{39}
\end{array}$

