Sketch a graph according to the question. In the sketch, we assume $k=3$.
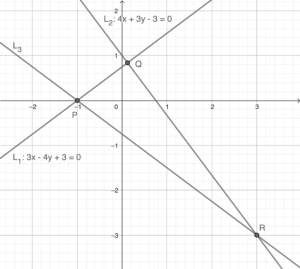
Note that the in-centre of $\Delta PQR$ lies on the $x$-axis. Then the $x$-axis is the angle bisector of $\angle QPR$. Hence, $PQ$ is the image of reflecting $L_1$ about the $x$-axis.
The equation of $L_1$ is
$\begin{array}{rcl}
3x-4y+k & = & 0 \\
4y & = & 3x+k \\
y & = & \dfrac{3x+k}{4}
\end{array}$
Therefore, the equation of $PR$ is
$\begin{array}{rcl}
y & = & -\left(\dfrac{3x+k}{4}\right) \\
y & = & \dfrac{-3x-k}{4}
\end{array}$
For the coordinates of $R$,
$\left\{ \begin{array}{ll}
4x+3y-k=0 & \ldots \unicode{x2460} \\
y=\dfrac{-3x-k}{4} & \ldots \unicode{x2461}
\end{array}\right.$
Sub. $\unicode{x2461}$ into $\unicode{x2460}$, we have
$\begin{array}{rcl}
4x+3\left(\dfrac{-3x-k}{4}\right)-k & = & 0 \\
4x+\dfrac{-9x-3k}{4}-k & = & 0 \\
16x -9x-3k-4k & = & 0 \\
7x & = & 7k \\
x & = & k
\end{array}$

