Sketch the graph according to the question.
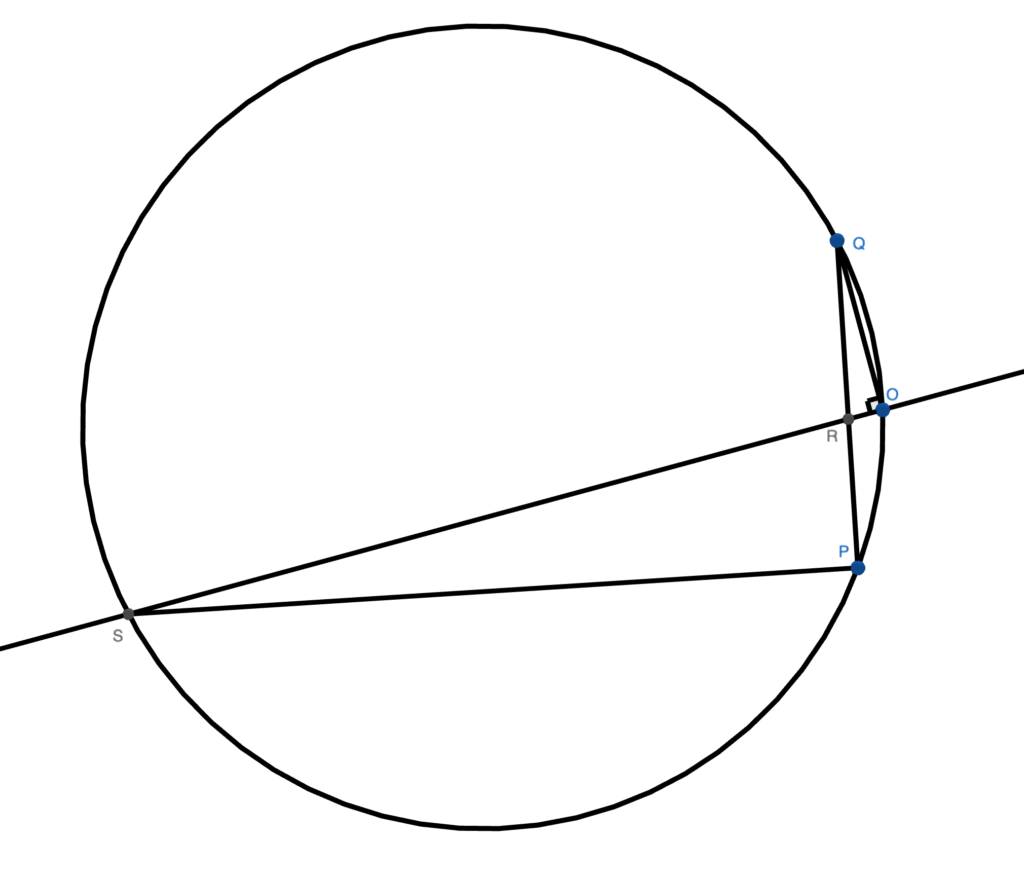
- Let $PR:RQ=1:\lambda$.
In $\Delta OPQ$, by section formula, we have
$\begin{array}{rcl}
\av{OR} & = & \dfrac{\lambda \av{OP}+\av{OQ}}{1+\lambda} \\
\av{OR} & = & \dfrac{\lambda(-2\bv{i}-\bv{k})+(2\bv{i}-\bv{j}+\bv{k})}{1+\lambda} \\
\av{OR} & = & \dfrac{2-2\lambda}{1+\lambda}\bv{i}-\dfrac{1}{1+\lambda}\bv{j}+\dfrac{1-\lambda}{1+\lambda}\bv{k}
\end{array}$Since $OR \perp OQ$, we have
$\begin{array}{rcl}
\av{OR} \cdot \av{OQ} & = & 0 \\
\dfrac{2-2\lambda}{1+\lambda}\bv{i}-\dfrac{1}{1+\lambda}\bv{j}+\dfrac{1-\lambda}{1+\lambda}\bv{k} \cdot (2\bv{i}-\bv{j}+\bv{k}) & = & 0 \\
\dfrac{2-2\lambda}{1+\lambda}\times 2+\dfrac{1}{1+\lambda}+\dfrac{1-\lambda}{1+\lambda} & = & 0 \\
4-4\lambda+1+1-\lambda & = & \\
-5\lambda+6 & = & 0 \\
\lambda & = & \dfrac{6}{5}
\end{array}$Hence, we have
$\begin{array}{rcl}
\av{OR} & = & \dfrac{2-2(\frac{6}{5})}{1+\frac{6}{5}}\bv{i}-\dfrac{1}{1+\frac{6}{5}}\bv{j}+\dfrac{1-\frac{6}{5}}{1+\frac{6}{5}}\bv{k} \\
\av{OR} & = & \dfrac{-2}{11}\bv{i}-\dfrac{5}{11}\bv{j}-\dfrac{1}{11}\bv{k}
\end{array}$ - Since $OR$ produced to $S$, then $O$, $R$ and $S$ are collinear. Hence, we have $\av{OS}=\mu \av{OR}$ for some real constant $\mu$.
$\begin{array}{rcl}
\av{OS} & = & \mu\av{OR} \\
\av{OS} & = & \dfrac{-2\mu}{11}\bv{i}-\dfrac{5\mu}{11}\bv{j}-\dfrac{\mu}{11}\bv{k}
\end{array}$Join $PQ$. By the theorem angle in the same segment, we have $\angle QPS = \angle QOS=90^\circ$. Therefore, we have $PQ\perp PS$. Hence, we have
$\begin{array}{rcl}
\av{PQ}\cdot \av{PS} & = & 0 \\
(\av{OQ}-\av{OP}) \cdot (\av{OS}-\av{OP}) & = & 0 \\
(4\bv{i}-\bv{j}+2\bv{k})\cdot(\left(\left(\dfrac{-2\mu}{11}+2\right) \bv{i}-\dfrac{5\mu}{11}\bv{j}+\left(\dfrac{-\mu}{11}+1\right)\bv{k}\right) & = & 0 \\
4\left(\dfrac{-2\mu}{11}+2\right)+\dfrac{5\mu}{11}+2\left(\dfrac{-\mu}{11}+1\right) & = & 0 \\
-8\mu+88+5\mu-2\mu+22 & = & 0 \\
-5\mu +110 & = & 0 \\
\mu & = & 22
\end{array}$Therefore, $\av{OS}=-4\bv{i}-10\bv{j}-2\bv{k}$.
-
- A required vector
$\begin{array}{cl}
= & \av{OP} \times \av{OQ} \\
= & \begin{vmatrix} \bv{i} & \bv{j} & \bv{k} \\ -2 & 0 & -1 \\ 2 & -1 & 1 \end{vmatrix} \\
= & \begin{vmatrix} 0 & -1 \\ -1 & 1 \end{vmatrix}\bv{i} -\begin{vmatrix} -2 & -1 \\ 2 & 1 \end{vmatrix}\bv{j} +\begin{vmatrix} -2 & 0 \\ 2 & -1 \end{vmatrix}\bv{k} \\
= & -\bv{i}+2\bv{k}
\end{array}$ - Sketch the graph according to the question.
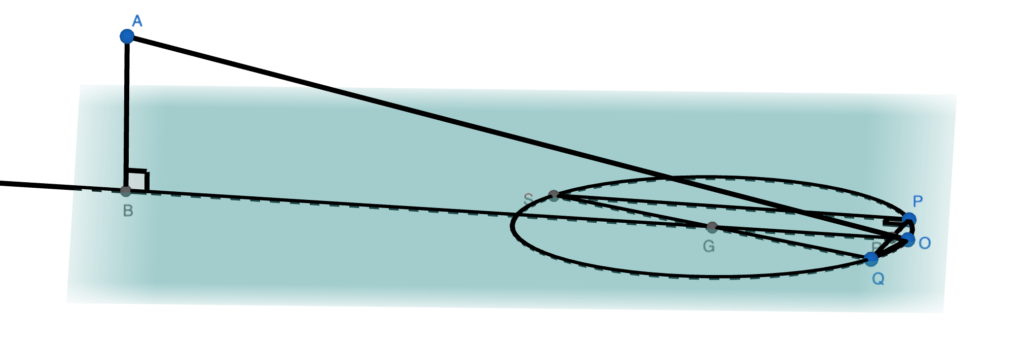
Since $\angle QOS=90^\circ$, then by the converse of angle in semi-circle, $QS$ is a diameter. Hence, we have
$\begin{array}{rcl}
\av{OG} & = & \dfrac{1}{2}(\av{OS}+\av{OQ}) \\
\av{OG} & = & \dfrac{1}{2}(-4\bv{i}-10\bv{j}-2\bv{k}+2\bv{i}-\bv{j} +\bv{k}) \\
\av{OG} & = & -\bv{i}-\dfrac{11}{2}\bv{j}-\dfrac{1}{2}\bv{k}
\end{array}$Since $\av{BA}$ is perpendicular to the plane $\Pi$, then $\av{BA} \text{//} (\av{OP}\times \av{OQ})$. Then by the formula of vector projection, we have
$\begin{array}{rcl}
\av{BA} & = & \dfrac{\av{OA}\cdot(\av{OP}\times \av{OQ})}{|\av{OP}\times \av{OQ}|} \left( \dfrac{\av{OP}\times \av{OQ}}{|\av{OP}\times \av{OQ}|}\right) \\
\av{BA} & = & \dfrac{(-6\bv{i}-22\bv{j}+2\bv{k})\cdot (-\bv{i}+2\bv{k})}{| -\bv{i}+2\bv{k}| } \left( \dfrac{-\bv{i}+2\bv{k}}{|-\bv{i}+2\bv{k}|}\right) \\
\av{BA} & = & \dfrac{(-6)(-1)+(-22)(0)+(2)(2)}{\sqrt{(-1)^2+(0)^2+(2)^2}} \left( \dfrac{-\bv{i}+2\bv{k}}{\sqrt{(-1)^2+(0)^2+(2)^2}}\right) \\
\av{BA} & = & 2(-\bv{i}+2\bv{k}) \\
\av{BA} & = & -2\bv{i}+4\bv{k}
\end{array}$Then, we have
$\begin{array}{rcl}
\av{OB} & = & \av{OA}-\av{BA} \\
\av{OB} & = & (-6\bv{i}-22\bv{j}+2\bv{k}) -(-2\bv{i}+4\bv{k}) \\
\av{OB} & = & -4\bv{i}-22\bv{j}-2\bv{k} \\
\av{OB} & = & 4\left(-\bv{i}-\dfrac{11}{2}\bv{j}-\dfrac{1}{2}\bv{k}\right) \\
\av{OB} & = & 4 \av{OG}
\end{array}$Hence, $O$, $B$ and $G$ are collinear.
- A required vector

