Angles at the Centre – Solving Master

Equal arcs imply the angles at the centre equal.

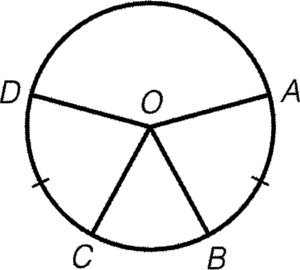
Condition: $\overparen{AB}=\overparen{CD}$

Result: $\angle AOB = \angle COD$

Reference: eq. arcs, eq. $\angle$s
Equal angles at centre imply the corresponding arcs equal in length.

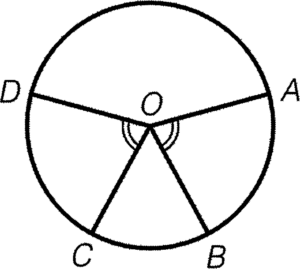
Condition: $\angle AOB = \angle COD$

Result: $\overparen{AB} = \overparen{CD}$

Reference: eq. $\angle$s, eq. arcs
Equal chords imply equal angles at the centre.

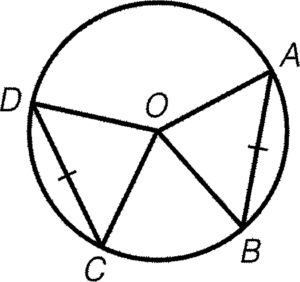
Condition: $AB=CD$

Result: $\angle AOB= \angle COD$

Reference: eq. chords, eq. $\angle$s
Equal angles at centre imply the corresponding chords equal in length.

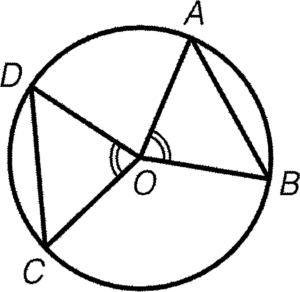
Condition: $\angle AOB=\angle COD$

Result: $AB=CD$

Reference: eq. $\angle$s, eq. chords
Equal chords imply the corresponding arcs equal in length.

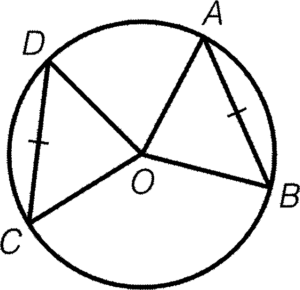
Condition: $AB=CD$

Result: $\overparen{AB}=\overparen{CD}$

Reference: eq. chords, eq. arcs
Equal arcs imply the corresponding chords equal in length.

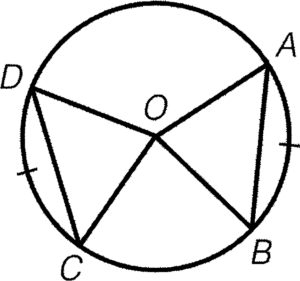
Condition: $\overparen{AB}=\overparen{CD}$

Result: $AB=CD$

Reference: eq. arcs, eq. chords
The lengths of arcs are proportional to the sizes of the angles at centre.

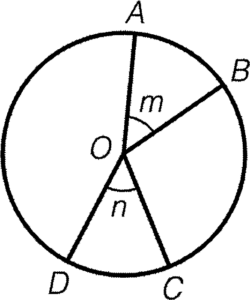
Result: $\overparen{AB}:\overparen{CD}=m:n$

Reference: arc and $\angle$ at centre in prop.