2021-II-02
$\begin{array}{rcl}
m(m-a) & = & a(1-m) \
$\begin{array}{rcl}
m(m-a) & = & a(1-m) \
$\begin{array}{cl}
& (u+v)(v-u)(u-1) \\
= �
$\begin{array}{cl}
& \dfrac{6}{n-6} –
For the accuracy correct to 2 decimal places, the maxi
$\begin{array}{rcl}
a(x+3)+b(3x+1) & \equiv
It is given that $f(x)=(x+h)(x-3) +k$.
$\begin{arra
Let $p(x) = (x^2-1)Q(x) +(ax+b)$, where $Q(x)$ is a po
The sum of the percentage of overweight girls and the p
Consider the first inequality, we have
$\begin{arra
$\begin{array}{rcl}
\dfrac{2\alpha+3\beta}{3\a
Let $w=\dfrac{kx^2}{y^3}$, where $k$ is a non-zero c
$\begin{array}{rcl}
T(1) & = & 3 \\
T(2) &#
Write the equation of the graph to the general form and
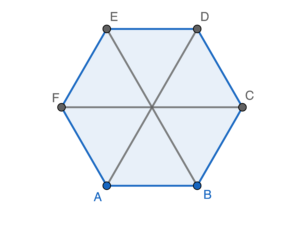
Note that the regular $6$-sided polygon can be divide
Let $r_1 \text{ cm}$ and $r_2 \text{ cm}$ be the radius
I is true. Let $r\text{ cm}$ be the radius of the sector
In $\Delta CDE$,
$\begin{array}{rcll}
\angle CED &#
I is true. Since $ABCD$ is a rectangle, then $AB\text{
Since $\Delta EBF \sim \Delta DAE$, then we have
$\beg
I is true.
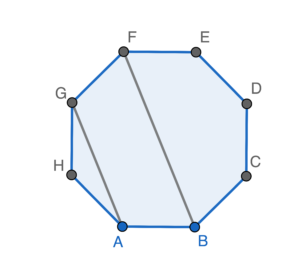
$\begin{array}{rcl}
\angle ABC & = &#
