2021-II-01
Ans: B
… Read $\begin{array}{cl}
& \dfrac{(2^n)(8^{3n})}
HKDSE-MATH - 2021 - Paper 2
2021-II-02
Ans: C
… Read $\begin{array}{rcl}
m(m-a) & = & a(1-m) \
2021-II-03
Ans: D
… Read $\begin{array}{cl}
& (u+v)(v-u)(u-1) \\
= �
2021-II-04
Ans: B
… Read $\begin{array}{cl}
& \dfrac{6}{n-6} –
2021-II-05
Ans: D
… Read For the accuracy correct to 2 decimal places, the maxi
2021-II-06
Ans: B
… Read $\begin{array}{rcl}
a(x+3)+b(3x+1) & \equiv
2021-II-07
Ans: A
… Read It is given that $f(x)=(x+h)(x-3) +k$.
$\begin{arra
2021-II-08
Ans: B
… Read Let $p(x) = (x^2-1)Q(x) +(ax+b)$, where $Q(x)$ is a po
2021-II-09
Ans: A
… Read The sum of the percentage of overweight girls and the p
2021-II-10
Ans: C
… Read Consider the first inequality, we have
$\begin{arra
2021-II-11
Ans: C
… Read $\begin{array}{rcl}
\dfrac{2\alpha+3\beta}{3\a
2021-II-12
Ans: B
… Read Let $w=\dfrac{kx^2}{y^3}$, where $k$ is a non-zero c
2021-II-13
Ans: C
… Read $\begin{array}{rcl}
T(1) & = & 3 \\
T(2) &#
2021-II-14
Ans: A
… Read Write the equation of the graph to the general form and
2021-II-15
Ans: C
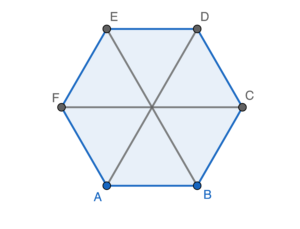
… Read Note that the regular $6$-sided polygon can be divide
2021-II-16
Ans: A
… Read Let $r_1 \text{ cm}$ and $r_2 \text{ cm}$ be the radius
2021-II-17
Ans: B
… Read I is true. Let $r\text{ cm}$ be the radius of the sector
2021-II-18
Ans: B
… Read In $\Delta CDE$,
$\begin{array}{rcll}
\angle CED &#
2021-II-19
Ans: D
… Read I is true. Since $ABCD$ is a rectangle, then $AB\text{
2021-II-20
Ans: C
… Read Since $\Delta EBF \sim \Delta DAE$, then we have
$\beg