2022-II-13
Ans: B
… Read Let $u=\dfrac{k\sqrt{v}}{w}$, where $k\neq 0$.
I is
HKDSE-MATH
2022-II-14
Ans: C
… Read $\begin{array}{rcl}
T(1) & = & 8 \\
T(2) &#
2022-II-15
Ans: A
… Read Let $r\text{ cm}$ be the radius of the the hemisphere.
2022-II-16
Ans: D
… Read Let $O$ be the centre of the circle. $A$ and $B$ be the en
2022-II-17
Ans: B
… Read Join $PN$.
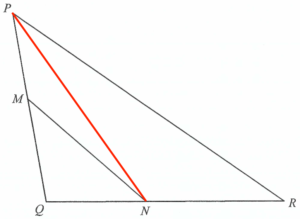
Let $x\text{ cm}^2$ be the area of $\Delta M
2022-II-18
Ans: C
… Read Since $ABCD$ is a rectangle, then we have
$\begin{arr
2022-II-19
Ans: D
… Read In $\Delta ABD$ and $\Delta CAE$,
$\begin{array}{rc
2022-II-20
Ans: B
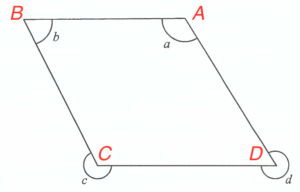
… Read Denote the four vertices by $A$, $B$, $C$ and $D$ as sho
2022-II-21
Ans: B
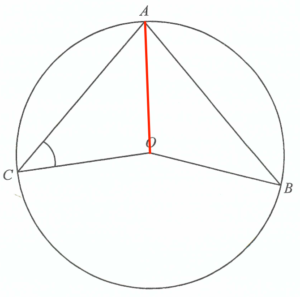
… Read Join $OA$.
$\begin{array}{rcll}
\angle CAB & =
2022-II-22
Ans: C
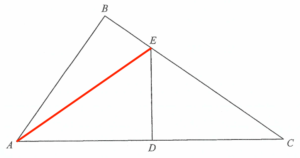
… Read Join $AE$. Since $\angle ABE = 90^\circ$ and $ABED$ is
2022-II-23
Ans: C
… Read Sketch the figure according to the question.
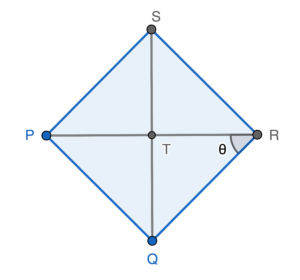
Since $P
2022-II-24
Ans: A
Rewrite the equation into slope intercept form, we ha
… Read Rewrite the equation into slope intercept form, we ha
2022-II-25
Ans: D
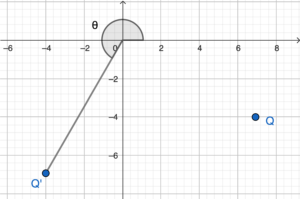
… Read Note that the rectangular coordinates of the image $Q
2022-II-26
Ans: A
… Read Note that the $x$- and $y$-intercepts of the $12x-5y=
2022-II-27
Ans: C
… Read Let $x^2+y^2+Dx+Ey+F=0$ be the equation of $C$. Sinc
2022-II-28
Ans: D
… Read Since only $532$ is divisible by $7$. Then the require
2022-II-29
Ans: A
… Read Let $x\text{ kg}$ be the mean weight of the actresses.
2022-II-30
Ans: B
… Read Since the median of the integers is $6$, then $x \ge 6$.
2022-II-31
Ans: C
… Read $\begin{array}{rcl}
\log (-345)^{768} & = �
2022-II-32
Ans: C
… Read By intercepts form, we have
$\begin{array}{rcl}
\df