- A pair of opposite angles of cyclic quadrilateral are supplement.
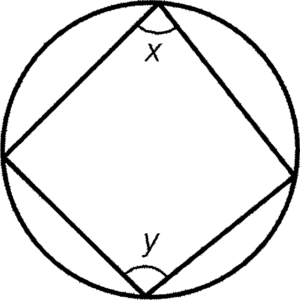
Condition: Two opposite angles of cyclic quadrilateral
Result: $x+y=180^\circ$
Reference: opp. $\angle$s, cyclic quad.
- If a pair of opposite angles of a quadrilateral are supplement, then the four vertexes are concyclic.
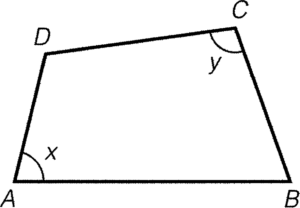
Condition: $\angle BAD + \angle BCD=180^\circ$
Result: $A$, $B$, $C$ and $D$ are concyclic.
Reference: opp. $\angle$s supp
- In a cyclic quadrilateral, an interior angle equals to the exterior opposite angle.
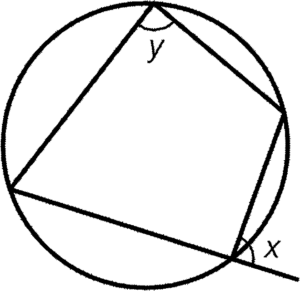
Condition: A cyclic quadrilateral
Result: $x=y$
Reference: ext. $\angle$, cyclic quad.
- If an interior angle equals to the exterior opposite angle of an quadrilateral, then the four vertexes are concyclic.
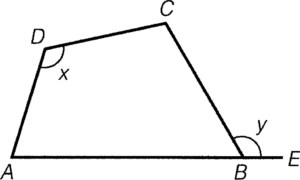
Condition: $\angle ADC=\angle CBE$
Result: $A$, $B$, $C$ and $D$ are concyclic
Reference: ext. $\angle$ eq int. opp. $\angle$
Resources for HKDSE Mathematics
