2006-II-46
Ans: B
In $\Delta OBC$,
… Read In $\Delta OBC$,
$\begin{array}{ll}
OB=OC & \t
$\begin{array}{ll}
OB=OC & \t
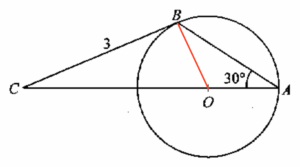
In $\Delta OAB$,
$\begin{array}{ll}
OB = B
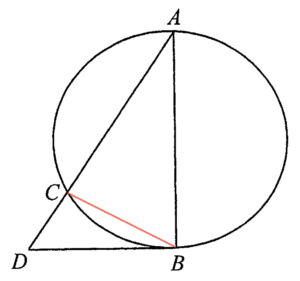
Join $BC$. Consider $\Delta ABD$ and $\Delta ACB$,
$\
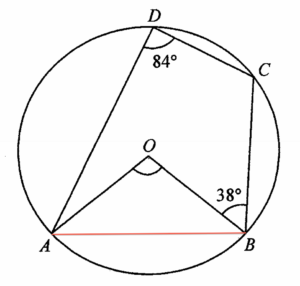
Join $AB$. Since $A$, $B$, $C$ and $D$ are four points o
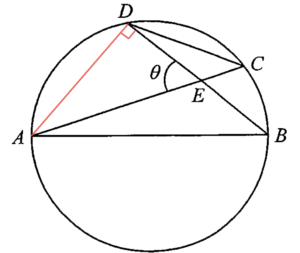
Join $AD$. Since $AB$ is a diameter of the circle $ABCD
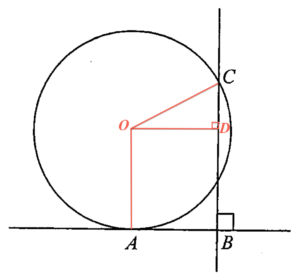
Denote $O$ the centre of the circle. Add a perpendicul
$\begin{array}{rcl}
\angle FA
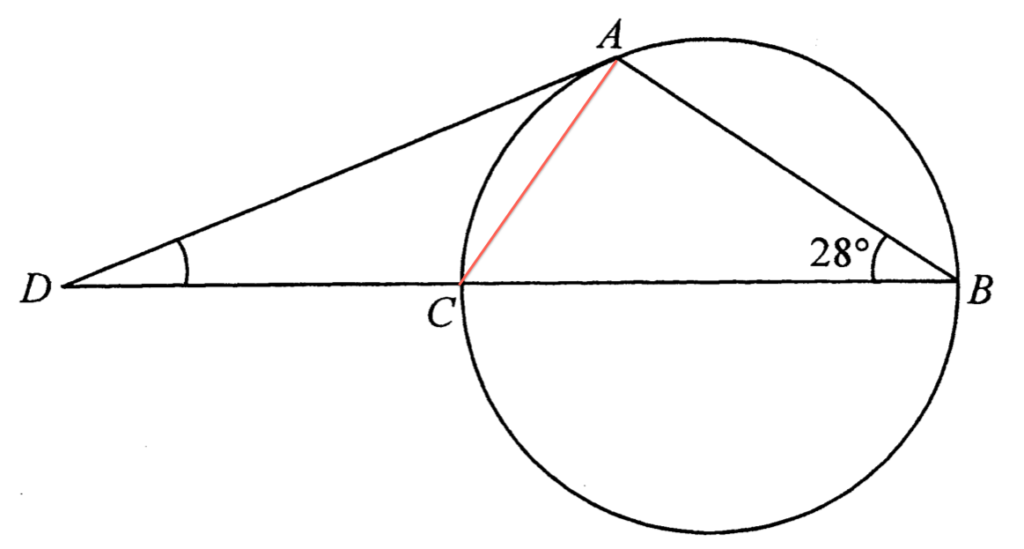
Since $DA$ is the tangent to the circle at $A
$\begin{array}{rcl}
$\therefore \angle AC
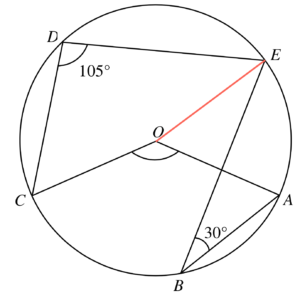
$\begin{array}{rcl}
\angle AOE & = &
$\begin{array}{rcl}
\angle TAC �
$\begin{array}{rcl}
\mbox{reflex }\ang
