2012-II-41
Ans: C
… Read Join $OB$.
$\begin{array}{rcl}
\angle BOQ & = &
HKDSE-MATH - 2012 - Paper 2 -
2012PP-I-07
Ans: $18^\circ$
$\begin{array}{rcl}
\angle BAC & = &
… Read $\begin{array}{rcl}
\angle BAC & = &
2012PP-I-14
Ans: (a) $\Delta DBC \sim \Delta DOA$ (b) (i) $(0,4)$ (ii) $(
… Read 2012PP-II-20
Ans: C
In $\Delta ABD$,
… Read In $\Delta ABD$,
$\because AB$ is the diameter,
$\the
2012PP-II-21
Ans: C
Join $OB$ and $OC$. Let $\angle COD = x$.
… Read Join $OB$ and $OC$. Let $\angle COD = x$.
$\because \ov
2012PP-II-40
Ans: C
Let $AD=AF=r\mbox{ cm}$.
… Read Let $AD=AF=r\mbox{ cm}$.
Since $AD$ is a radius of the
2013-II-19
Ans: C
$\because AB//AD$,
… Read $\because AB//AD$,
$\therefore \angle ADB = \angle D
2013-II-41
Ans: D
Join $BC$.
… Read Join $BC$.
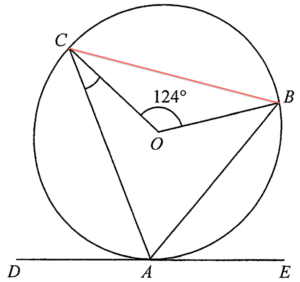
$\begin{array}{rcl}
\angle BAC & = &
2014-II-20
Ans: B
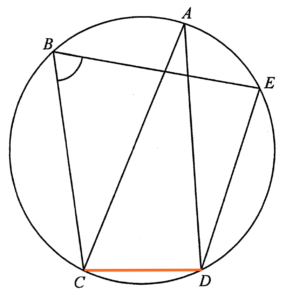
… Read Join $CD$. Since $AC$ is a diameter, then $\angle ADC =
2014-II-21
Ans: A
Since $AB=CD=EF$, then the distances between the cen
… Read Since $AB=CD=EF$, then the distances between the cen
2014-II-41
Ans: C
Since $I$ is the in-centre of $\Delta QRS$, then we hav
… Read Since $I$ is the in-centre of $\Delta QRS$, then we hav
2015-II-20
Ans: C
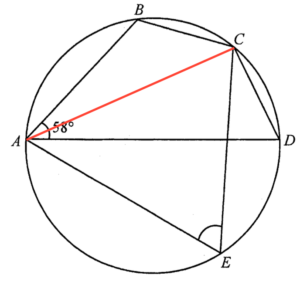
… Read Join $AC$.
$\begin{array}{ll}
BC = CD & \text{(
2015-II-21
Ans: B
… Read Since $AC$ and $BD$ are diameters of the circle, then t
2015-II-40
Ans: C
Since $BD$ is a diameter of the circle, then we have
… Read Since $BD$ is a diameter of the circle, then we have
$\b
2016-II-22
Ans: D
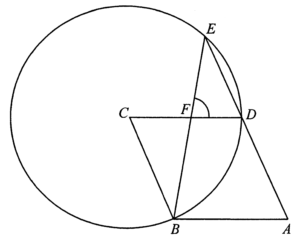
… Read Since $ABCD$ is a rhombus, then we have $BC\text{//}A
2016-II-40
Ans: D
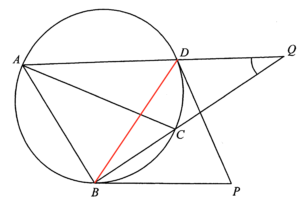
… Read Join $BD$. Consider $\Delta PBD$, we have
$\begin{ar
2017-II-21
Ans: C
Join $AC$.
… Read Join $AC$.
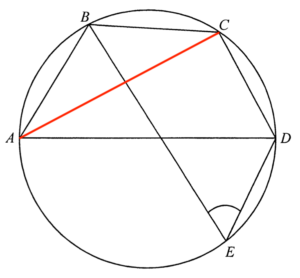
In quadrilateral $ABCD$,
$\begin{array}
2017-II-40
Ans: B
Join $AC$.
… Read Join $AC$.
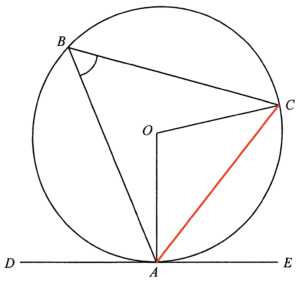
Since $DE$ is the tangent to the circle at $A