Tangents to a Circle

11-07-2023 app.cch No Comments

If $PQ$ is a tangent to the circle at $T$, then $OT$ is perpendicular to $PQ$.

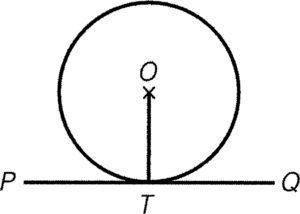
Condition: $PQ$ is a tangent at $T$

Result: $OT \perp PQ$

Reference: tangent $\perp$ radius
If $OT$ is perpendicular to $PTQ$, then $PQ$ is a tangent to the circle at $T$.

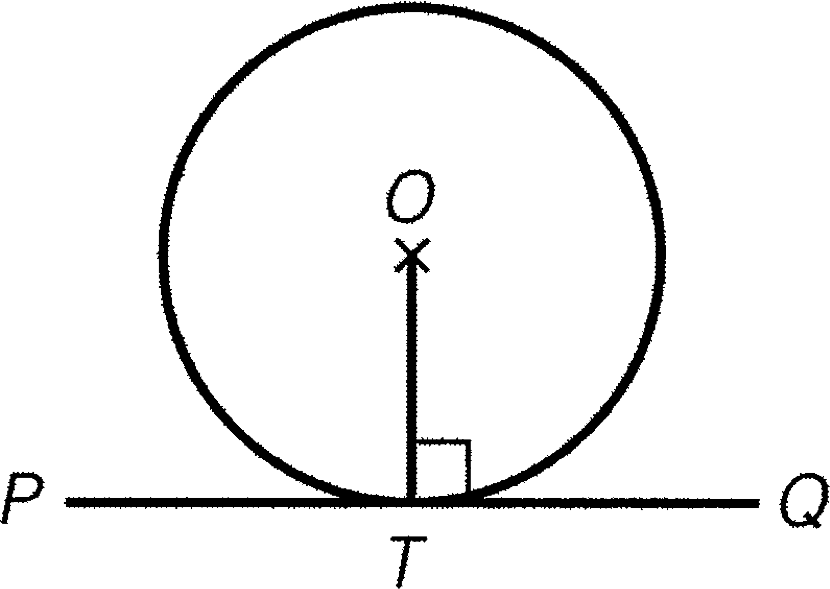
Condition: $OT\perp PTQ$

Result: $PQ$ is a tangent

Reference: converse of tangent $\perp$ radius
If $PQ$ is a tangent to the circle at $T$, any straight line perpendicular to $PQ$ and passing through $T$ must pass through the centre.

Condition: $PQ$ is a tangent at $T$ and a perpendicular line passing through $T$

Result: The straight line must pass through the centre

Reference: line passing through the pt of contact $\perp$ tangent passes through centre
Given that $PT$ and $QT$ are two tangents to the same circle. Then $\Delta OPT \cong \Delta OQT$.

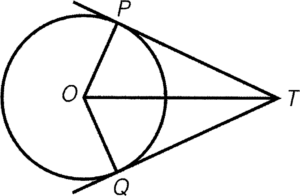
Condition: Two tangents $PT$ and $QT$

Result:
1. $PT=QT$
2. $\angle PTO=\angle QTO$
3. $\angle TOP = \angle TOQ$
Reference: tangent properties
If $PQ$ is a tangent to the circle, then the angles in alternate segment equal.

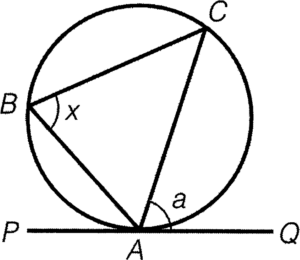
Condition: $PQ$ is a tangent

Result: $\angle ABC = \angle CAQ$

Reference: $\angle$ in alt. segment
If the angles in the alternate segment equal, then $PQ$ is a tangent to the circle at $A$.

Condition: $\angle ABC=\angle CAQ$

Result: $PQ$ is a tangent to the circle

Reference: converse of $\angle$ in alt. segment

Math, Measures, Shape and Space, Properties of Circle, Revision Note

Leave a Reply Cancel reply