圓內接四邊形

Posted on By app.cch 在〈圓內接四邊形〉中尚無留言
  1. 圓內接四邊形的內對角必定互補。

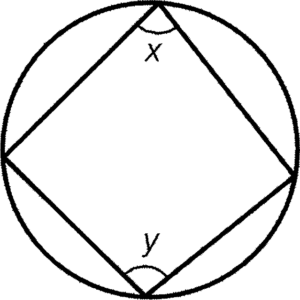
    條件：兩隻圓內接四邊形的內對角

    結論：$x+y=180^\circ$

    簡記：圓內接四邊形的內角

  2. 若一個四邊形其中一對內對角互補，則該四邊形的頂點必定共圓。

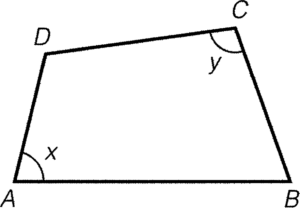
    條件：$\angle BAD + \angle BCD=180^\circ$

    結論：$A$、$B$、$C$ 及 $D$ 共圓

    簡記：對角互補

  3. 在一圓內接四邊形中，內角與其外對角必定相等。

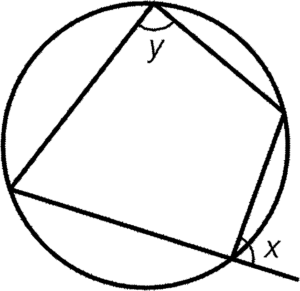
    條件：圓內接四邊形

    結論：$x=y$

    簡記：圓內接四邊形的外角

  4. 若一個四邊形的內角與其外對角相等，則該四邊形的頂點必定共圓。

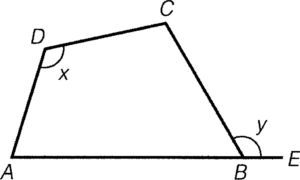
    條件：$\angle ADC=\angle CBE$

    結論：$A$、$B$、$C$ 及 $D$ 共圓

    簡記：外角等於內對角

Same Topic:

Default Thumbnail圓周角 Default Thumbnail弦 Default Thumbnail特殊角的三角比 Default Thumbnail餘弦公式
圓的性質, 度量、圖形與空間, 數學, 溫習筆記

發佈留言

發佈留言必須填寫的電子郵件地址不會公開。 必填欄位標示為 *