圓周角 – Solving Master

圓心角的大小必定為它所對應的圓周角大小的兩倍。

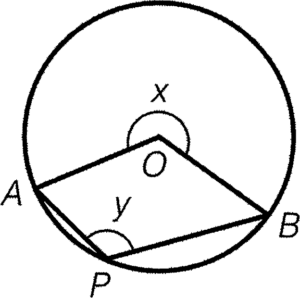
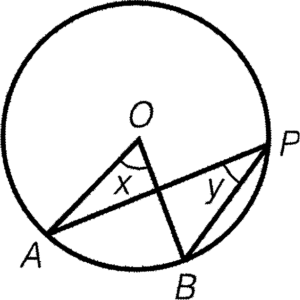
結論：$x=2y$

簡記：圓心角兩倍於圓周角
若 $AB$ 為圓的一直徑，且 $P$ 為圓周上的一點，則 $\angle APB$ 必定為直角。

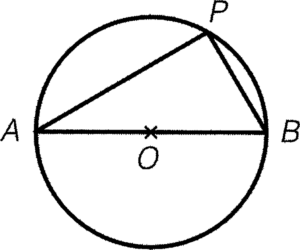
條件：$AB$ 為一直徑

結論：$\angle APB=90^\circ$

簡記：半圓上的圓周角
若 $\angle APB$ 為一直角，則 $AB$ 必定為圓的一直徑。

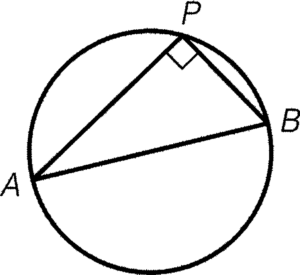
條件：$\angle APB=90^\circ$

結論：$AB$ 為圓的一直徑

簡記：半圓上的圓周角的逆定理
同一個弓形內的所有圓周角必定相等。

結論：$x=y$

簡記：同弓形內的圓周角
若 $\angle ADB$ 和 $\angle ACB$ 相等，則 $A$、$B$、$C$ 及 $D$ 必定共圓。

條件：$\angle ADB=\angle ACB$

結論：$A$、$B$、$C$ 及 $D$ 共圓

簡記：同弓形內的圓周角的逆定理
兩個圓周角大小之比，與其對應之弧長之比必定相同。

結論：$\overparen{AB}:\overparen{CD} = x:y$

簡記：弧長與圓周角成比例