- 對於兩條長度相等的弧，其對應的圓心角必定相等。
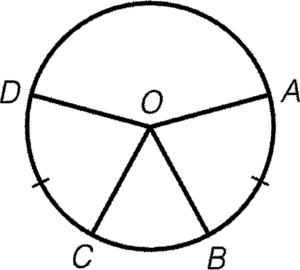
條件：$\overparen{AB}=\overparen{CD}$
結論：$\angle AOB = \angle COD$
簡記：等弧對等角
- 對於兩個相等的圓心角，其對應的弦的長度必定相等。
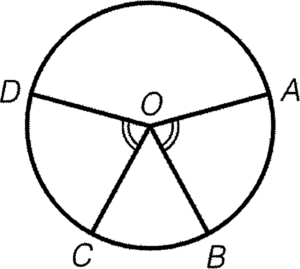
條件：$\angle AOB = \angle COD$
結論：$\overparen{AB}=\overparen{CD}$
簡記：等角對等弧
- 對於兩條相等的弦，其對應的圓心角必定相等。
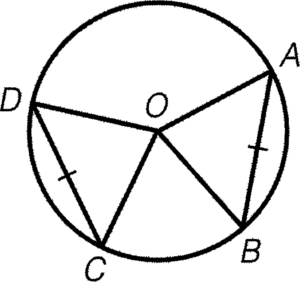
條件：$AB=CD$
結論：$\angle AOB= \angle COD$
簡記：等弦對等角
- 對於兩個相等的圓心角，其對應的弦的長度必定相等。
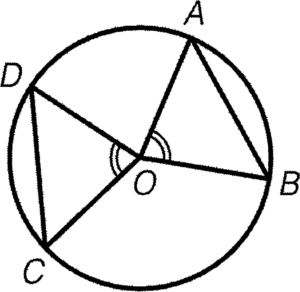
條件：$\angle AOB=\angle COD$
結論：$AB=CD$
簡記：等角對等弦
- 對於兩條相等的弦，其對應的弧的長度必定相等。
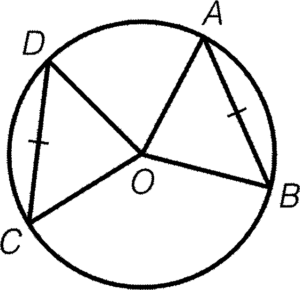
條件：$AB=CD$
結論：$\overparen{AB}=\overparen{CD}$
簡記：等弦對等弧
- 對於兩條相等長度的弧，其對應的弦的長度必定相等。
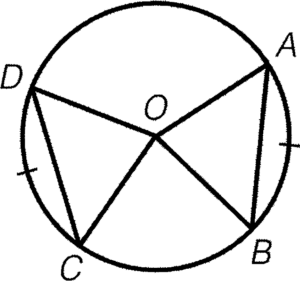
條件：$\overparen{AB}=\overparen{CD}$
結論：$AB=CD$
簡記：等弧對等弦
- 兩條弧的長度之比，與其對應角的大小之比必定相同。
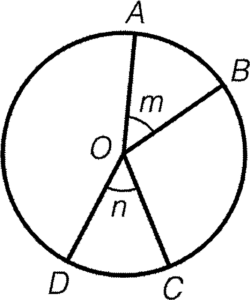
結論：$\overparen{AB}:\overparen{CD}=m:n$
簡記：弧長與圓心角成比例
Resources for HKDSE Mathematics
