- 垂直弦且通過圓心的直線必定平分弦。
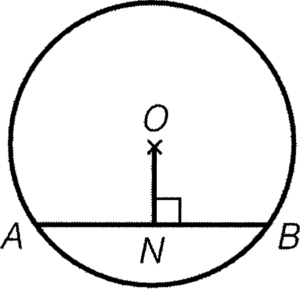
條件：$ON\perp AB$
結論：$AN=BN$
簡記：圓心至弦的垂線平分弦
- 連結圓心及弦的中點的直線必定垂直弦。
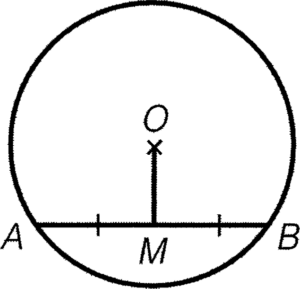
條件：$AM=MB$
結論：$OM\perp AB$
簡記：圓心至弦的中點的連線垂直弦
- 弦的垂直平分線必定通過圓心。
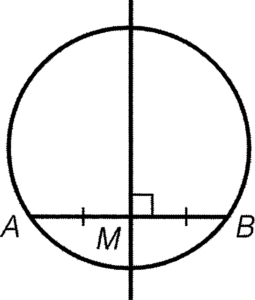
簡記：弦的垂直平分線通過圓心
- 對於兩條相等的弦，它們與圓心的必定距離相等。
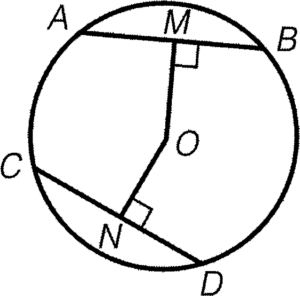
條件：$AB=CD$
結論：$OM=ON$
簡記：等弦與圓心等距
- 對於兩條與圓心有相同距離的弦，它們必定相等。
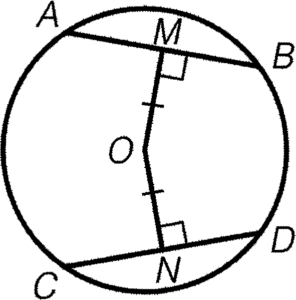
條件： $OM=ON$
結論： $AB=CD$
簡記：與圓心等距的弦等長
Resources for HKDSE Mathematics
