2006-I-13

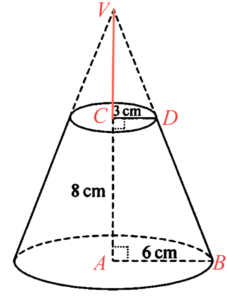
留意 $\Delta VCD \sim \Delta VAB$。所以，可得

$\begin{array}{rcl}
\dfrac{VC}{VA} & = & \dfrac{CD}{AB} \\
\dfrac{VC}{VC+8} & = & \dfrac{3}{6} \\
VC & = & 8 \text{ cm}
\end{array}$

所以，固體 $X$ 的體積

$\begin{array}{cl}
= & \dfrac{1}{3} \pi (6)^2 (16) – \dfrac{1}{3} \pi (3)^2 (8) + \dfrac{2}{3} \pi (6)^3 \\
= & 312\pi \text{ cm}^3
\end{array}$

由於固體 $X$ 與固體 $Y$ 相似，可得

$\begin{array}{rcl}
\dfrac{\text{固體 $X$ 的體積}}{\text{固體 $Y$ 的體積}} & = & \left( \dfrac{\text{固體 $X$ 的表面面積}}{\text{固體 $Y$ 的表面面積}} \right)^\frac{3}{2} \\
\dfrac{312\pi}{\text{固體 $Y$ 的體積}} & = & \left( \dfrac{4}{9} \right) ^\frac{3}{2} \\
\dfrac{312\pi}{\text{固體 $Y$ 的體積}} & = & \dfrac{8}{27} \\
\text{固體 $Y$ 的體積} & = & 1053 \pi \text{ cm}^3
\end{array}$

可是，

$\begin{array}{rcl}
\dfrac{\text{固體 $X’$ 的體積}}{\text{固體 $Y’$ 的體積}} & = & \dfrac{312\pi + \frac{4}{3}\pi(1)^3}{1053\pi + \frac{4}{3}\pi(2)^3} \\
& = & \dfrac{940}{3191} \\
& \neq & \dfrac{1}{8}
\end{array}$

所以，它們不相似。