-
- 由於 $H$ 為 $\Delta ABC$ 的垂心,則 $AO\perp BC$。由此,可得 $\angle AOC = 90^\circ$。
由於 $BS$ 為圓的一直徑,則可得
$\begin{array}{ll}
\angle BCS = 90^\circ & \text{(半圓上的圓周角)}
\end{array}$考慮 $AH$ 及 $SC$,
$\angle AOC + \angle BCS$
$\begin{array}{cl}
= & 90^\circ + 90^\circ \\
= & 180^\circ
\end{array}$$\therefore AH\text{//} SC$ (同旁內角互補)。
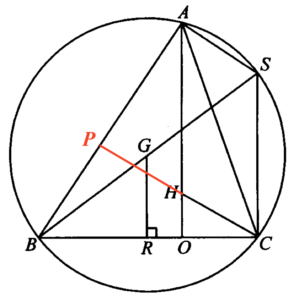
現在,把 $CH$ 延伸至 $AB$ 上的 $P$。由於 $H$ 為 $\Delta ABC$ 垂心,則 $CP \perp AB$。由此,可得 $\angle CPA=90^\circ$。
由於 $BS$ 為圓的一直徑,則可得
$\begin{array}{ll}
\angle BAS = 90^\circ & \text{(半圓上的圓周角)}
\end{array}$考慮 $CH$ 及 $SA$,
$\angle CPA + \angle BAS$
$\begin{array}{cl}
= & 90^\circ + 90^\circ \\
= & 180^\circ
\end{array}$$\therefore CH\text{//} SA$ (同旁內角互補)。
由於 $AH\text{//} SC$ 及 $CH\text{//} SA$,所以 $AHCS$ 為一平行四邊形。
- 已知 $G$ 為圓心,且 $GR \perp BC$。由此,可得
$\begin{array}{ll}
BR = RC & \text{(圓心至圓的垂線平分圓)}
\end{array}$在 $\Delta BCS$ 中,
$\begin{array}{ll}
BG = GS & \text{(半徑)} \\
BR = RC & \text{(已證)}
\end{array}$$\therefore SC = 2RG$ (中點定理)。
根據 (a)(i) 的結果,可得
$\begin{array}{ll}
AH = SC & \text{(// 四邊形的對邊)}
\end{array}$由此,可得 $AH=2GR$。
- 由於 $H$ 為 $\Delta ABC$ 的垂心,則 $AO\perp BC$。由此,可得 $\angle AOC = 90^\circ$。
-
- 設 $x^2 +y^2 +Dx +Ey +F=0$ 為所求圓形的方程。由於該圓通過 $A$、$B$ 及 $C$,則可把 $A$、$B$ 及 $C$ 的坐標代入至該圓的方程。由此,可得
$\left\{ \begin{array}{l}
(0)^2 + (12)^2 +D(0) + E(12) +F =0 \\
(-6)^2 + (0)^2 +D(-6) + E(0) +F =0 \\
(4)^2 + (0)^2 +D(4) +E(0) +F =0
\end{array}\right.$$\left\{ \begin{array}{ll}
12E + F = -144 & \ldots \unicode{x2460} \\
-6D + F = -36 & \ldots \unicode{x2461} \\
4D + F = -16 & \ldots \unicode{x2462}
\end{array}\right.$$\unicode{x2462} – \unicode{x2461}$,可得
$\begin{array}{rcl}
10D & = & 20 \\
D & = & 2
\end{array}$把 $D=2$ 代入 $\unicode{x2462}$,可得
$\begin{array}{rcl}
4(2) + F & = & -16 \\
F & = & -24
\end{array}$把 $F=-24$ 代入 $\unicode{x2460}$,可得
$\begin{array}{rcl}
12E + (-24) & = & -144 \\
12E & = & -120 \\
E & = & -10
\end{array}$所以,所求的方程為 $x^2 +y^2 +2x – 10y -24=0$。
- 留意 $H$ 在正 $y$ 軸之上,設 $H=(0,y)$。由於 $H$ 為 $\Delta ABC$ 的垂心,可得 $AB\perp CH$。由此,可得
$\begin{array}{rcl}
m_{AB} \times m_{CH} & = & -1 \\
\dfrac{12 – 0}{0 – (-6)} \times \dfrac{y-0}{0-4} & = & -1 \\
\dfrac{y}{-2} & = & -1 \\
y & = & 2
\end{array}$所以,$H=(0,2)$。
- 根據 (b)(i) 的結果,$G=(-1,5)$。考慮
$m_{GH} \times m_{BG}$
$\begin{array}{cl}
= & \dfrac{5-2}{-1-0} \times \dfrac{5-0}{-1-(-6)} \\
= & -3 \\
\neq & -1
\end{array}$所以,$GH\not \perp BG$。由此,可得 $\angle BGH \neq 90^\circ$。
因為 $H$ 為 $\Delta ABC$ 的垂心,所以 $HO \perp BC$。
由此,可得 $\angle HOB = 90^\circ$。所以,$\angle BGH + \angle HOB \neq 180^\circ$。
由此,$B$、$O$、$H$ 及 $G$ 不是共圓。
- 設 $x^2 +y^2 +Dx +Ey +F=0$ 為所求圓形的方程。由於該圓通過 $A$、$B$ 及 $C$,則可把 $A$、$B$ 及 $C$ 的坐標代入至該圓的方程。由此,可得
2006-I-16
答案:(b) (i) $x^2+y^2+2x-10y-24=0$ (ii) $(0,2)$

