答案:C
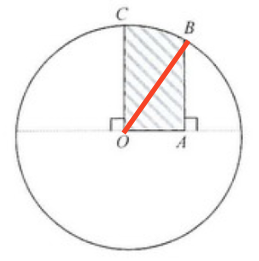

連結 $OB$。由於 $OC$ 及 $OB$ 均為半徑,則 $OB = 2\text{ cm}$。在 $\Delta OAB$ 中,
$\begin{array}{rcl}
\cos \angle BOA & = & \dfrac{OA}{OB} \\
\cos \angle BOA & = & \dfrac{1}{2} \\
\angle BOA & = & 60^\circ
\end{array}$
由此,可得
$\begin{array}{rcl}
\angle BOC & = & 90^\circ – \angle BOA \\
& = & 30^\circ
\end{array}$
在 $\Delta OAB$ 中利用畢氏定理,可得
$\begin{array}{rcl}
AB^2 & = & OB^2 – OA^2 \\
AB & = & \sqrt{2^2 – 1^2} \\
AB & = & \sqrt{3} \text{ cm}
\end{array}$
所以,陰影部分 $OABC$ 的面積
$\begin{array}{cl}
= & \pi (2)^2 \times \dfrac{30^\circ}{360^\circ} + \dfrac{1}{2} \times 1 \times \sqrt{3} \\
= & \left(\dfrac{\pi}{3} + \dfrac{\sqrt{3}}{2} \right) \text{ cm}^2
\end{array}$

