答案:C
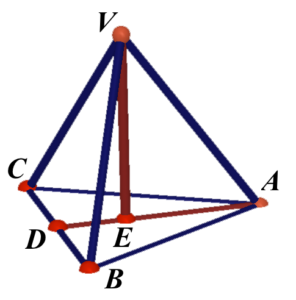

留意正四面體的每個面均為邊長為 $3\text{ cm}$ 的等邊三角形。考慮其底三角形 $ABC$。在 $BC$ 上加點 $D$ 使得 $AD\perp BC$ 及 $BD=CD$。留意 $E$ 為 $\Delta ABC$ 的形心。
$\begin{array}{rcl}
AC^2 & = & AD^2 + CD^2 \\
(3)^2 & = & AD^2 + (1.5)^2 \\
AD & = & \dfrac{3\sqrt{3}}{2} \text{ cm}
\end{array}$
因為 $E$ 為 $\Delta ABC$ 的形心,$AE:ED = 2:1$。由此,可得 $AE = \sqrt{3}\text{ cm}$。在 $\Delta VEA$ 中,
$\begin{array}{rcl}
VA^2 & = & VE^2 + AE^2 \\
VE^2 & = & (3)^2 – (\sqrt{3})^2 \\
VE^2 & = & 6 \\
VE & = & \sqrt{6} \text{ cm}
\end{array}$
所以,該正四面體的高為 $\sqrt{6}\text{ cm}$。

