答案:B
連結 $OB$。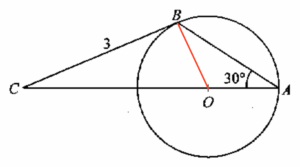
連結 $OB$。

在 $\Delta OAB$ 中,
$\begin{array}{ll}
OB = BA & \text{(半徑)} \\
\angle OBA = \angle OAB & \text{(等腰 $\Delta$ 的底角)} \\
\angle OBA = 30^\circ & \\
\end{array}$
$\begin{array}{ll}
\angle BOC = \angle OBA + \angle OAB & \text{($\Delta$ 的外角)} \\
\angle BOC = 30^\circ + 30^\circ & \\
\angle BOC = 60^\circ & \\
\end{array}$
在 $\Delta OBC$ 中,
$\begin{array}{ll}
\angle OBC =90^\circ & \text{(半徑 $\perp$ 切線)}
\end{array}$
由此,可得
$\begin{array}{rcl}
\tan \angle BOC & = & \dfrac{BC}{OB} \\
\tan 60^\circ & = & \dfrac{3}{OB} \\
OB & = & \dfrac{3}{\tan 60^\circ} \\
OB & = & \sqrt{3}
\end{array}$

