2007-I-11

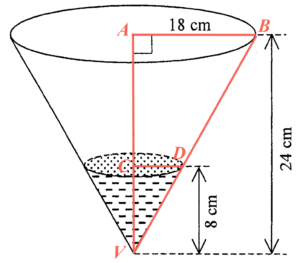
留意 $\Delta VAB \sim \Delta VCD$。則可得

$\begin{array}{rcl}
\dfrac{VC}{VA} & = & \dfrac{CD}{AB} \\
\dfrac{8}{24} & = & \dfrac{CD}{18} \\
CD & = & 6 \text{ cm}
\end{array}$

所以，該圓錐形容器內水的底半徑為 $6\text{ cm}$。由此，該容器內的水的體積

$\begin{array}{cl}
= & \dfrac{1}{3} \times \pi \times 6^2 \times 8 \\
= & 96\pi \text{ cm}^3
\end{array}$

1. 容器內的水的斜高 $VD$

   $\begin{array}{cl}
   = & \sqrt{6^2 + 8^2} \\
   = & 10\text{ cm}
   \end{array}$

   所以，容器內被浸濕的曲面面積

   $\begin{array}{cl}
   = & \pi \times 6 \times 19 \\
   = & 60\pi \text{ cm}^2
   \end{array}$

2. 留意較大的容器與原本容器相似，所以較大容器被浸濕的曲面面積也是 $60\pi\text{ cm}^2$。