2007-I-16

$\begin{array}{rcl}
s & = & \dfrac{AB + BC + AC}{2} \\
& = & \dfrac{9 + 5 + 6}{2} \\
& = & 10 \text{ cm}
\end{array}$

所以，三角形底 $ABC$ 的面積

$\begin{array}{cl}
= & \sqrt{s(s-AB)(s-BC)(s-AC)} \\
= & \sqrt{10(10-9)(10-5)(10-6)} \\
= & \sqrt{200} \\
= & 10\sqrt{2} \text{ cm}^2
\end{array}$

由此，紀念品 $ABCDEF$ 的體積

$\begin{array}{cl}
= & 10\sqrt{2} \times 20 + \dfrac{1}{3}\times 10\sqrt{2} (23-20) \\
= & 200\sqrt{2} + 10\sqrt{2} \\
= & 210\sqrt{2} \text{ cm}^3
\end{array}$

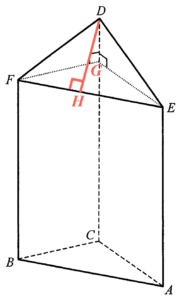
留意 $FG=BC=5\text{ cm}$、$GE=CA=6\text{ cm}$ 及 $EF=AB=9\text{ cm}$。在 $\Delta DFG$ 中，

$\begin{array}{rcl}
DF^2 & = & DG^2 +FG^2 \\
DF & = & \sqrt{3^2 + 5^2} \\
DF & = & \sqrt{34} \text{ cm}
\end{array}$

在 $\Delta DEG$，

$\begin{array}{rcl}
DE^2 & = & DG^2 + GE^2 \\
DE & = & \sqrt{3^2 + 6^2} \\
DE & = & \sqrt{45}\text{ cm}
\end{array}$

在 $\Delta DEF$ 運用餘弦公式，可得

$\begin{array}{rcl}
\cos \angle DFE & = & \dfrac{DF^2 + EF^2 – DE^2}{2(DF)(EF)} \\
\cos \angle DFE & = & 0.666\ 938\ 943 \\
\angle DFE & = & 48.168\ 751\ 76^\circ \\
\angle DFE & \approx & 48.2^\circ
\end{array}$

留意中 $D$ 至 $EF$ 的最短距離為 $DH$。在 $\Delta DFH$ 中，

$\begin{array}{rcl}
\sin \angle DFH & = & \dfrac{DH}{DF} \\
DH & = & DF\sin \angle DFH \\
DH & = & 4.344\ 714\ 399 \\
DH & = & 4.34 \text{ cm}
\end{array}$

$\begin{array}{cl}
= & 5 \times 4 \\
= & 20 \text{ cm}^2
\end{array}$

$\Delta DEF$ 的面積

$\begin{array}{cl}
= & \dfrac{1}{2} \times EF \times DH \\
= & 19.551\ 214\ 8 \text{ cm}^2 \\
< & 20 \text{ cm}^2 \end{array}$

所以，該矩形金屬薄片不可能固定在三角形表面 $DEF$ 上，使該金屬片完全在三角形 $DEF$ 內。