答案:B
加直線 $FX$ 使得 $AB//FX//CD$。由於 $AY$ 及 $CY$ 分別為 $\angle BAX$ 及 $\angle DCX$ 的角平分線,設 $\angle BAY = \angle YAX = \alpha$ 及 $\angle DCY = \angle YCX = \beta$。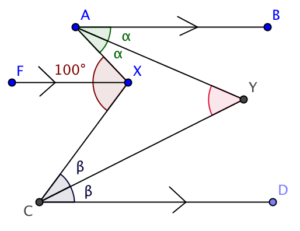
加直線 $FX$ 使得 $AB//FX//CD$。由於 $AY$ 及 $CY$ 分別為 $\angle BAX$ 及 $\angle DCX$ 的角平分線,設 $\angle BAY = \angle YAX = \alpha$ 及 $\angle DCY = \angle YCX = \beta$。

由於 $AB//FX$,可得
$\begin{array}{rcl}
\angle AXF & = & \angle BAX \\
\angle AXF & = & 2 \alpha
\end{array}$
由於 $FX//CD$,可得
$\begin{array}{rcl}
\angle FXC & = & \angle XCD \\
\angle FXC & = & 2\beta
\end{array}$
由此,可得
$\begin{array}{rcl}
\angle AXF + \angle FXC & = & \angle AXC \\
2\alpha + 2\beta & = & 100^\circ \\
2(\alpha + \beta) & = & 100^\circ \\
\alpha + \beta & = & 50^\circ
\end{array}$
考慮多邊形 $AXCY$,
$\begin{array}{rcl}
\text{反角 } AXC & = & 360^\circ – 100^\circ \\
\text{反角 } AXC & = & 260^\circ
\end{array}$
由於 $AXCY$ 為四邊形,可得
$\begin{array}{rcl}
\alpha + 260^\circ + \beta + \angle AYC & = & 360^\circ \\
50^\circ + 260^\circ + \angle AYC & = & 360^\circ \\
\angle AYC & = & 50^\circ
\end{array}$

