2008-I-13

$\begin{array}{rcl}
\overparen{ABC} & = & 2 \pi (20) \times \dfrac{216^\circ}{360^\circ} \\
& = & 240 \pi \text{ cm}
\end{array}$

留音該弧長相等於 $X$ 的底圓周。所以，可得

$\begin{array}{rcl}
2\pi r & = & 24\pi \\
r & = & 12
\end{array}$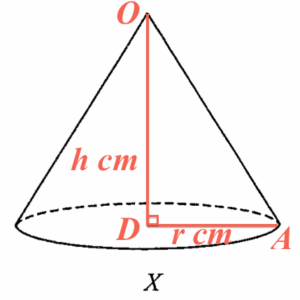

參考以上的圖像，透過利用畢氏定理於 $\Delta OAD$，可得

$\begin{array}{rcl}
OA^2 & = & OD^2 + DA^2 \\
20^2 & = & h^2 + 12^2 \\
h & = & \sqrt{400-144} \\
& = & 16
\end{array}$

所以，$X$ 的底半徑及高分別為 $12\text{ cm}$ 及 $16\text{ cm}$。

$\begin{array}{cl}
= & \dfrac{1}{3} \times \pi (12)^2 \times 16 \\
= & 768\pi \text{ cm}^3
\end{array}$

$\begin{array}{rcl}
2 \pi y & = & 2 \pi (10) \times \dfrac{108^\circ}{360^\circ} \\
y & = & 3
\end{array}$

由此，可得

$\begin{array}{rcl}
\dfrac{X\text{ 的底半徑}}{Y \text{ 的底半徑}} & = & \dfrac{12}{3} \\
& = & 4
\end{array}$

另外，可得

$\begin{array}{rcl}
\dfrac{OA}{PD} & = & \dfrac{20}{10} \\
& = & 2
\end{array}$

因為以上兩個比不相等，則 $X$ 及 $Y$ 並不相似。