2008-I-15

$\begin{array}{rcl}
\angle DBH + \angle DHB & = & \angle HDA \\
35^\circ + \angle DHB & = & 50^\circ \\
\angle DHB & = & 15^\circ
\end{array}$

留意 $BD=50\text{ m}$。透過利用正弦公式於 $\Delta BDH$，可得

$\begin{array}{rcl}
\dfrac{BD}{\sin \angle BHD} & = & \dfrac{BH}{\sin BDH} \\
\dfrac{50}{\sin 15^\circ} & = & \dfrac{BH}{\sin (180^\circ-50^\circ)} \\
BH & = & \dfrac{50\sin 130^\circ}{\sin 15^\circ} \\
& = & 147.988~422~3 \\
& \approx & 148 \text{ m}
\end{array}$

1. 透過利用餘弦公式於 $\Delta BCH$，可得

   $\begin{array}{rcl}
   \cos \angle CBH & = & \dfrac{BH^2 + BC^2 – CH^2}{2(BH)(BC)} \\
   & = & \dfrac{147.988~422~3^2 + 210^2 – 130^2}{2(147.988~422~3)(210)} \\
   & = & 0.789~968~057 \\
   \angle CBH & = & 37.817~473~47^\circ \\
   & \approx & 37.8^\circ
   \end{array}$

2. 

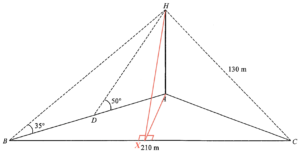
   在 $BC$ 上加點 $X$ 使得 $HX \perp BC$ 及 $AX \perp BC$。考慮 $\Delta BXH$，

   $\begin{array}{rcl}
   \sin \angle HBX & = & \dfrac{HX}{BH} \\
   \sin 37.817~473~47^\circ & = & \dfrac{HX}{147.988~422~3} \\
   HX & = & 90.738~804~95 \text{ m}
   \end{array}$

   考慮 $\Delta HAB$，

   $\begin{array}{rcl}
   \sin \angle HBA & = & \dfrac{HA}{BH} \\
   \sin 35^\circ & = & \dfrac{HA}{147.988~422~3} \\
   HA & = & 84.882~671~91 \text{ m}
   \end{array}$

   考慮 $\Delta HXA$，

   $\begin{array}{rcl}
   \sin \angle HXA & = & \dfrac{HA}{HX} \\
   & = & \dfrac{84.882~671~91}{147.988~422~3} \\
   & = & 0.935~461~646 \\
   \angle HXA & = & 69.302~855~61 \\
   & \approx & 69.3^\circ
   \end{array}$

   所以，所求的角為 $69.3^\circ$。

3. 留意 $HX \perp BC$ 及 $AX \perp BC$。所以，$HX$ 為平面 $HBC$ 上有最大斜率的直線。由此，在平面 $HBC$ 上最大的傾角為 $\angle HXA$ （即 $69.3^\circ$）。所以，在 $BC$ 上不能找到一點 $K$ 使得由 $K$ 測得 $H$ 的仰角為 $75^\circ$。