2008-I-17

$\begin{array}{ll}
\angle PAB = \angle PAC & \text{(內心)}
\end{array}$

由於 $A$、$B$、$P$ 及 $C$ 為圓周上的四點，則

$\begin{array}{ll}
\angle PAB = \angle PCB & \text{(同弓形上的圓周角)} \\
\angle PAC = \angle PBC & \text{(同弓形上的圓周角)}
\end{array}$

由此，可得 $\angle PBC = \angle PCB$。所以，可得

$\begin{array}{ll}
BP=CP & \text{(等角對等邊)}
\end{array}$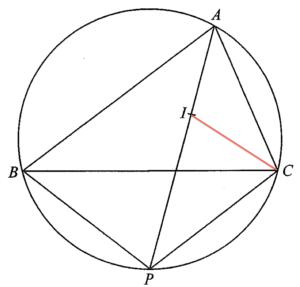

連結 $C$ 及 $I$。考慮 $\Delta ABC$，

$\begin{array}{ll}
\angle BCI = \angle ACI & \text{(內心)}
\end{array}$

另外，

$\begin{array}{ll}
\angle PAC = \angle PCB & \text{(已證)}
\end{array}$

由此，可得

$\begin{array}{ll}
\angle PCI & \\
= \angle PCB + \angle BCI & \\
= \angle PAC + \angle ACI & \text{(已證)} \\
= \angle PIC & \text{($\Delta$ 的外角)}
\end{array}$

所以，可得

$\begin{array}{ll}
CP=IP & \text{(等角對等邊)}
\end{array}$

由此，$BP=CP=IP$。

1. 留意 $G$ 為 $\Delta ABC$ 的外心，則 $GP$ 為 $BC$ 的垂直平分線。留意 $B$ 及均為 $x$ 軸上的點，則 $BC$ 為一水平線。由此，$G$ 和 $P$ 的 $x$ 坐標相等。$P$ 的 $x$ 坐標

   $\begin{array}{cl}
   = & \dfrac{-80 + 64}{2} \\
   = & -8
   \end{array}$

   設 $P=(-8, y)$。利用 (a) 的結果，可得

   $\begin{array}{rcl}
   BP & = & IP \\
   \sqrt{(-80-(-8))^2+(0-y)^2} & = & \sqrt{(0-(-8))^2 + (32-y)^2} \\
   5184 + y^2 & = & 64 + 1024 – 64y +y^2 \\
   64y & = & -4096 \\
   y & = & -64
   \end{array}$

   所以，$P=(-8,-64)$。所以，可得

   $\begin{array}{rcl}
   BP & = & \sqrt{(-80-(-8))^2 + (0-(-64))^2} \\
   & = & \sqrt{9280}
   \end{array}$

   由此，所求的方程為

   $\begin{array}{rcl}
   (x-(-8))^2 + (y-(-64))^2 & = & (\sqrt{9280})^2 \\
   x^2 +16x +64 + y^2 + 128y +4096 & = & 9280 \\
   x^2 +y^2 +16x + 128y – 5120 & = & 0
   \end{array}$

2. 設 $G=(-8,m)$。由於 $G$ 為 $\Delta ABC$ 的外心，則

   $\begin{array}{rcl}
   BG & = & GP \\
   \sqrt{(-80-(-8))^2 + (0-m)^2} & = & m-(-64) \\
   5184 + m^2 & = & (m+64)^2 \\
   5184 + m^2 & = & m^2 +128m +4096 \\
   128m & = & 1088 \\
   m & = & \dfrac{17}{2}
   \end{array}$

   所以，$G=(-8,\dfrac{17}{2})$。留意 $PQ$ 為直徑及 $G$ 為圓 $ABPC$ 的圓心。留意 $PQ$ 為鉛垂線。由此，設 $Q=(-8,n)$。則可得

   $\begin{array}{rcl}
   QG & = & PG \\
   n – \dfrac{17}{2} & = & \dfrac{17}{2} – (-64) \\
   n & = & 81
   \end{array}$

   所以，$Q=(-8,81)$。

3. $BQ$ 的斜率

   $\begin{array}{cl}
   = & \dfrac{81- 0}{-8-(-80)} \\
   = & \dfrac{9}{8}
   \end{array}$

   $QI$ 的斜率

   $\begin{array}{cl}
   = & \dfrac{81- 32}{-8-0} \\
   = & \dfrac{-49}{8}
   \end{array}$

   由於 $BQ$ 的斜率 $\times QI$ 的斜率 $\neq -1$，則 $\angle BQI \neq 90^\circ$。由此，$\angle BQI \neq \angle IRC$。所以，$B$、$Q$、$I$ 及 $R$ 並不共圓。