答案:C
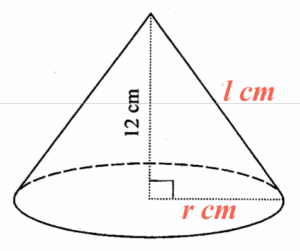

設 $r\text{ cm}$ 及 $l \text{ cm}$ 分別為底半徑及斜高。由於其底圓的周界 $18\pi\text{ cm}$,可得
$\begin{array}{rcl}
2 \pi r & = & 18 \pi \\
r & = & 9
\end{array}$
利運畢氏定理於該圓錐體,可得
$\begin{array}{rcl}
l^2 & = & 12^2 + r^2 \\
l & = & \sqrt{144 + 9^2} \\
& = & 15
\end{array}$
所以,該圓錐體的總表面面積
$\begin{array}{cl}
= & \pi \times (9) \times (15) + \pi \times (9)^2 \\
= & 216 \pi \text{ cm}^2
\end{array}$

