答案:B
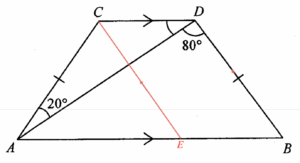

設 $\angle ADC = y$。在 $AB$ 上加點 $E$ 使得 $EC//BD$。留意 $CEBD$ 為一平行四邊形,可得
$\begin{array}{rcl}
\angle CEB & = & \angle CDB \\
& = & y + 80^\circ
\end{array}$
由於 $AEB$ 為一直線,可得
$\begin{array}{rcl}
\angle CEA & = & 180^\circ – \angle CEB \\
& = & 180^\circ – (y+80^\circ) \\
& = & 100^\circ – y
\end{array}$
由於 $CD//AB$,則 $\angle DAB = y$。
因為 $CEBD$ 為一平行四邊形,所以,$EC = BD$。所以,$AC = EC$。由此,可得
$\begin{array}{rcl}
\angle CAE & = & \angle CEA \\
y + 20^\circ & = & 100^\circ – y \\
2y & = & 80^\circ \\
y & = & 40^\circ
\end{array}$

