答案:D
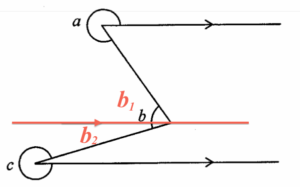

加入一水平線,該線把 $b$ 分為 $b_1$ 及 $b_2$ 兩角,參考上圖。利用平行線的性質,可得 $a+b_1=360^\circ$ 及 $c+b_2=360^\circ$。
A 可能錯誤。假定 $a=315^\circ$、$b_1=45^\circ$、$b_2=15^\circ$ 及 $c=345^\circ$。明顯地 $a+b_1=360^\circ$ 及 $c+b_2=360^\circ$,但 $a+b \neq c$。
B 可能錯誤。假定 $a=315^\circ$、$b_1=45^\circ$、$b_2=15^\circ$ 及 $c=345^\circ$。明顯地 $a+b_1=360^\circ$ 及 $c+b_2=360^\circ$,但 $a+b \neq c+ 90^\circ$。
C 可能錯誤。假定 $a=315^\circ$、$b_1=45^\circ$、$b_2=15^\circ$ 及 $c=345^\circ$。明顯地 $a+b_1=360^\circ$ 及 $c+b_2=360^\circ$,但 $a+c \neq b + 540^\circ$。
D 必為正確。由於 $a+b_1=360^\circ$ 及 $c+b_2=360^\circ$,可得
$\begin{array}{rcl}
(a +b_1) + (c+b_2) & = & 360^\circ + 360^\circ \\
a + (b_1 + b_2) + c & = & 720^\circ \\
a + b + c & = & 720^\circ
\end{array}$

