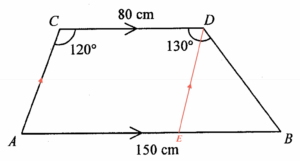
在 $AB$ 上加點 $E$ 使得 $AC//ED$。則 $AEDC$ 為一平行四邊形。因為 $AC // ED$,可得
$\begin{array}{rcl}
\angle ACD + \angle CDE & = & 180^\circ \\
120^\circ + \angle CDE & = & 180^\circ \\
\angle CDE & = & 60^\circ
\end{array}$
因為 $CD//AB$,可得
$\begin{array}{rcl}
\angle DEB & = & \angle CDE \\
& = & 60^\circ
\end{array}$
由於 $AEDC$ 為一平行四邊形,則 $AE=CD$。由此,可得
$\begin{array}{rcl}
EB & = & AB – AE \\
& = & 150 – 80 \\
& = & 70\text{ cm}
\end{array}$
考慮 $\Delta BED$,
$\begin{array}{rcl}
\angle EDB & = & 130^\circ – \angle CDE \\
& = & 130^\circ – 60^\circ \\
& = & 70^\circ
\end{array}$
由此,利用正弦公式於 $\Delta BED$,可得
$\begin{array}{rcl}
\dfrac{BD}{\sin \angle BED} & = & \dfrac{EB}{\sin \angle EDB} \\
\dfrac{BD}{\sin 60^\circ} & = & \dfrac{70}{\sin70^\circ} \\
BD & = & \dfrac{70\sin 60^\circ}{\sin 70^\circ} \\
& = & 64.512~348~96 \\
& \approx & 65\text{ cm}
\end{array}$

