2009-I-13

$\begin{array}{cl}
= & \dfrac{1}{3} \times \pi (12)^2 \times 18 \\
= & 864\pi \text{ cm}^3
\end{array}$

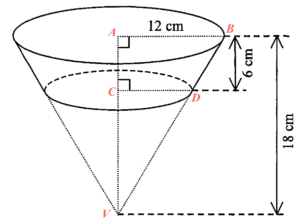
因為 $\Delta VAB \sim \Delta VCD$，可得

$\begin{array}{rcl}
\dfrac{VA}{VC} & = & \dfrac{AB}{CD} \\
\dfrac{18}{18-6} & = & \dfrac{12}{CD} \\
CD & = & 8\text{ cm}
\end{array}$

所以，該平截頭體的體積

$\begin{array}{cl}
= & 864\pi – \dfrac{1}{3}\times \pi (8)^2 \times 12 \\
= & 608\pi \text{ cm}^3
\end{array}$

$\begin{array}{cl}
= & \pi (8)^2 \times 10 \\
= & 640\pi \text{ cm}^3
\end{array}$

所以，在該器皿上半部分平截頭體的水的體積

$\begin{array}{cl}
= & 884\pi – 640 \pi \\
= & 244 \pi \text{ cm}^3
\end{array}$

由於該器皿上半部分的平截頭體及其內的水所形成的平截頭體並不相似，我們必須考慮最原本的圓錐形容器。

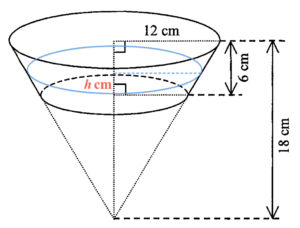
由於整個圓錐形容器與水加上在 (a)(ii) 部被切去的部分的總和相似，可得

$\begin{array}{rcl}
\dfrac{\text{容器的容量}}{\text{水與被切去部分的總體積}} & = & \left(\dfrac{18}{12 + h} \right)^3 \\
\dfrac{864\pi}{244 + \frac{1}{3} \times \pi (8)^2 \times 12} & = & \left(\dfrac{18}{12+h}\right)^3 \\
\dfrac{864\pi}{500\pi} & = & \left(\dfrac{18}{12+h} \right)^3 \\
\dfrac{6}{5} & = & \dfrac{18}{12+h} \\
12 + h & = & 18 \times \dfrac{6}{5} \\
12 + h & = & 15 \\
h & = & 3
\end{array}$

所以，水在平截頭體內的水深為 $3\text{ cm}$。由此，水在該器皿的水深

$\begin{array}{cl}
= & 10 + 3 \\
= & 13\text{ cm}
\end{array}$

$\begin{array}{cl}
= & 608\pi – 244 \pi \\
= & 364 \pi \\
= & 1~143.539~726 \text{ cm}^3 \\
> & 1~000 \text{ cm}^3
\end{array}$

所以，水不會溢出。