答案:C
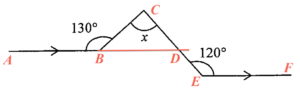

$AB$ 的延線交 $CE$ 於 $D$。由於 $ABD$ 為一直線,可得
$\begin{array}{rcl}
\angle CBD & = & 180^\circ – 130^\circ \\
& = & 50^\circ
\end{array}$
因為 $AD//EF$,可得
$\begin{array}{rcl}
\angle BDE & = & \angle DEF \\
& = & 120^\circ
\end{array}$
考慮 $\Delta BCD$,可得
$\begin{array}{rcl}
\angle CBD + \angle BCD & = & \angle BDE \\
50^\circ + x & = & 120^\circ \\
x & = & 70^\circ
\end{array}$

