答案:B
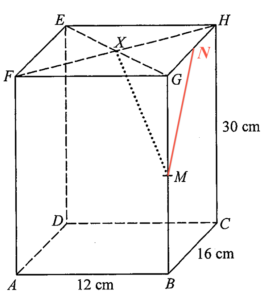

設 $N$ 為 $HG$ 的中點。則直線 $MX$ 與平面 $BCHG$ 的交角為 $\angle XMN$。利用畢氏定理於 $\Delta MNG$,可得
$\begin{array}{rcl}
MN^2 & = & MG^2 + GN^2 \\
MN & = & \sqrt{15^2 + 8^2} \\
& = & 17 \text{ cm}
\end{array}$
留意 $XN = 6\text{ cm}$。考慮 $\Delta XMN$,可得
$\begin{array}{rcl}
\tan \angle XMN & = & \dfrac{XN}{MN} \\
\tan \theta & = & \dfrac{6}{17}
\end{array}$

