答案:B
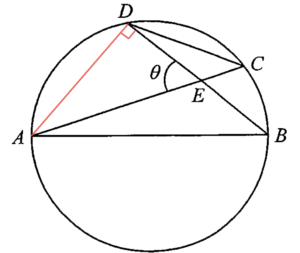

連結 $AD$。由於 $AB$ 為圓 $ABCD$ 的一直徑,則 $\angle ADB = 90^\circ$。考慮 $\Delta ADE$,可得 $\cos\theta =\dfrac{DE}{AE}$。
考慮 $\Delta ABE$ 及 $\Delta DCE$,
$\begin{array}{ll}
\angle AEB = \angle DEC & \text{(對頂角)} \\
\angle EAB = \angle EDC & \text{(同弓形內的圓周角)} \\
\angle EBA = \angle ECD & \text{(同弓形內的圓周角)}
\end{array}$
所以,$\Delta ABE \sim \Delta DCE$ (AAA)。由此,可得
$\begin{array}{rcl}
\dfrac{CD}{AB} & = & \dfrac{DE}{AE} \\
& = & \cos \theta
\end{array}$

