答案:C
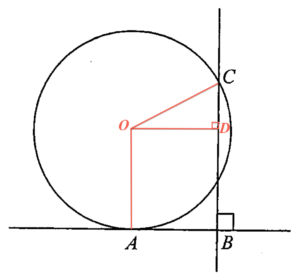

標示 $O$ 為該圓的圓心。加一垂線 $BC$ 及通過 $O$ 的直線,並標示 $D$ 為該交點。設 $r$ 為該圓的半徑。留意 $OA = BD = OC = r$ 及 $OD = AB = 20$。利用畢氐定理於 $\Delta OCD$,可得
$\begin{array}{rcl}
OC^2 & = & OD^2 + CD^2 \\
r^2 & = & 20^2 + (50-r)^2 \\
r^2 & = & 400 + 2500-100r +r^2 \\
100r & = & 2900 \\
r & = & 29
\end{array}$

