答案:C
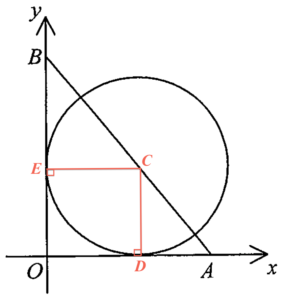

標示 $C$ 為該圓的圓心。設 $D$ 及 $E$ 分別為 $OA$ 及 $OB$ 的切點。設 $r$ 為該圓的半徑。留意 $CD = CE = OE = OD = r$,也留意 $C$ 的坐標為 $(r,r)$。由於 $A$ 的坐標為 $(21,0)$,則 $OA = 21$。也由於 $B$ 的坐標為 $(0,28)$,則 $OB=28$ 及 $BE = 28 -r$。留意 $\Delta OAB \sim \Delta ECB$,則可得
$\begin{array}{rcl}
\dfrac{OA}{EC} & = & \dfrac{OB}{EB} \\
\dfrac{21}{r} & = & \dfrac{28}{28-r} \\
21(28-r) & = & 28r \\
588 – 21r & = & 28r \\
49r & = & 588 \\
r & = & 12
\end{array}$
所以,該圓的半徑為 $12$ 且其圓心的坐標為 $(12,12)$。由此,該圓的方程為
$\begin{array}{rcl}
(x-12)^2 + (y-12)^2 & = & 12^2 \\
x^2 -24x +144 + y^2 -24y + 144 & = & 144 \\
x^2 +y^2 -24x – 24y +144 & = & 0
\end{array}$

