2010-I-09

答案：(a) $126^\circ$

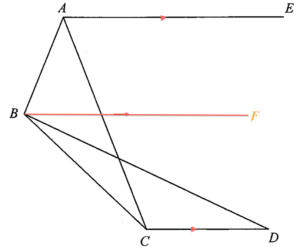
加上直線 $BF$，使得 $AE//BF//CD$，如上圖所示。

1. 由於 $AE//BF$，則

   $\begin{array}{rcl}
   \angle BAE + \angle ABF & = & 180^\circ \\
   108^\circ + \angle ABF & = & 180^\circ \\
   \angle ABF & = & 72^\circ
   \end{array}$

   由於 $BF//CD$，則

   $\begin{array}{rcl}
   \angle CBF + \angle BCD & = & 180^\circ \\
   \angle CBD + 126^\circ & = & 180^\circ \\
   \angle CBD & = & 54^\circ
   \end{array}$

   由此，可得

   $\begin{array}{rcl}
   \angle ABC & = & \angle ABF + \angle CBF \\
   & = & 72^\circ + 54^\circ \\
   & = & 126^\circ
   \end{array}$

2. 在 $\Delta ABC$ 和 $\Delta DCB$ 中，

   $\begin{array}{ll}
   BC = CB & \text{(公共邊)} \\
   AB = DC & \text{(已知)} \\
   \angle ABC = \angle BCD = 126^\circ & \text{(已證)}
   \end{array}$

   $\therefore \Delta ABC \cong \Delta DCB$(S.A.S)。